Form and Function of MOA and MIL
TLDR
- MIL single-digit rounding is more comfortable and faster.
- Dialing MILs is simpler.
- Speed Dope is useful in many applications.
- MILS align to range much simpler than MOA
- WIND in MILs is far easier than in MOA.
Introduction
When it comes to long-range precision shooting, the debate between MIL and MOA scopes can feel as old as time. Articles continue to pop up saying the exact same thing, never daring to step out of the well-worn track of last week’s article on the same subject. Most of these articles are filled with mathematical gobbledygook, and others don’t dare offend one camp or the other. The common responses often leave so much to be desired that I find myself wishing I had the time back from reading the latest article to spend doing something more useful – like watching YouTube.
So instead of waiting for the next version of the exact same thing, we are going to write what we have wanted to read but never found. Let’s break down the origins, modern applicability, and practical advantages of MIL and MOA with the precision we expect from our rifles, and not leave ourselves saying “the wind screwed us” again.

Relevant (to me) Background
To continue the debate between MIL and MOA scopes let’s look at the origins. Originating from the radian, the MIL (milliradian) is a base-10 angular measurement. Contrary to popular belief, MILs are NOT just “the metric system,” making it as comfortable with yards and miles per hour (MPH) as your average American is with inches, hot dogs, and ketchup. Often poised in opposition to the MIL, the MOA, derived from degrees, has long been associated with the imperial system, particularly inches.
Historically entrenched in U.S. shooting sports and firearms calibration, MOA carries the heavy burden of tradition, much like that old iron sight rifle your grandfather insists is still the best and can hit a target at 800 yards just as well as any of the newfangled ones. I’m tired of the dogma eating my homework, and this time I’m handing it in – in all CAPS.
MOA is a comfort zone of complacency and is entrenched in our common language – even for MIL users. We talk about the accuracy of a rifle in its MOA (inches) group size. When zeroing a rifle and spotting for your buddy, we often still talk in “you were ½ inch high and 1 inch right.” To the casual shooter – the occasional hunter or long-range plinker with buddies at the range – the gravitational pull of the MOA scope that works in “inches” still has an appeal. That’s totally OK, and MOA scopes work just as accurately and reliably as MIL scopes.
Some shooters might even argue that because MOA scope “clicks” adjust the angle of measurement at a finer scale (.25” at 100 yards for MOA versus .36 inches at 100 yards for MIL), the MOA scopes are more accurate. Garbage – well, MAYBE we can see how this might be useful in ELR shooting – but then again, those competitors often opt for scopes with even finer gradations of 1/8 MOA.

Gradations
Let’s look at the gradations:
- 1st click – .25 vs .36 – .11 difference
- 2nd click – .5 vs .72 – .22 difference
- 3rd click – .75 – in MILs you would just use 2 clicks .72 – .03 difference
- 4th click – 1.0 – MILs 3 clicks 1.08 – .08 difference
- 5th click – 1.25 – MILs 4 clicks 1.44 = .19 difference
- 6th click – 1.5 – MILs 4 clicks 1.44 = .06 difference
So, the most difference you get is .22 and the average difference in fidelity is .11. But this difference is completely devoid of the reality of ballistic calculations at distance. It assumes that the ballistic adjustment needed is always in perfect .25 inch increments – and it’s not.
Real Distances
Let’s look at real random distances you might have to shoot and its relevance to the debate between MIL and MOA scopes. We are going to stick to the standard American civilian shooter working in yards because that is where the debate occurs. It does not occur in the military because they woke up to the advantage of MILs long ago since they faced life-or-death choices and don’t have the luxury of fanciful debates.
- 430 yards – 32.92 inches = 7.31 MOA = 2.13 MIL
- 560 yards – 67.37 inches = 11.49 MOA = 3.34 MIL
- 785 yards – 164.84 inches = 20.69 MOA = 6.08 MIL
(ShootersCalculator.com – G7 – .310bc – 140 grain – 100 yd zero – 2.48 sight height, 0 wind)

Let’s Get Nerdy
So, at 430 yards, as an MOA shooter, your closest dial is 7.25 – meaning your dial point is off by .06, or 24% of a click, or .06 of an inch out of 32.92 inches – .18% – not even 1%. Can you shoot that difference at 430 yards?
For MILs, your dial point is 2.1, so you are 30% off a click value, or .08 of an inch out of 32.92 inches = .24% – a quarter of a percent. Can you shoot that difference at 430 yards?
If your gun consistently shoots a .5-inch group, then your error in dial ability is a minuscule fraction of your group size. The dialing difference is completely masked in the noise of your group. So even if MOA has a finer gradient of dialing, does it really matter? Even so, we’ll give the nod to MOA.
One thing should be abundantly clear by now for both MIL and MOA. You better get comfortable with rounding in a lot of your shooting. Many of us that get into precision shooting gravitate to the word “precision” and are compulsive about finding the perfect and exact ballistic solution, the perfect ammo load, or thinking we can derive perfect environmental and wind readings. As much as our typical compulsion for precise answers drives us, this sport humbles us to get comfortable accepting inherent variables and the reality of rounding.

Advantages of MIL
Now let’s get into the real advantages of MIL. And you make the choice if you would trade the below advantages for the finer gradient of MOA.
Ease of 1 Digit Rounding vs 2 Digit Rounding
When your ballistic app or Kestrel gives you a ballistic solution – elevation – it is usually in 2 digits – e.g., 6.37. If you have to round that to just one decimal place, what is the answer – 6.4. That rounding is super easy on us mentally; we all are used to doing this in our lives.
If you have to round this same number 6.37 to its nearest 2-digit answer of .25 or .50 – what is your answer? Regardless of which you chose – 6.25 or 6.50 – most of us took a moment longer to choose because the .12 spread and 2-digit resolution is a bit more challenging mentally.
Even if you say, “that’s not fair,” what if the number is 6.35? Now the MIL shooter also has a dilemma of which way to dial – 6.3 or 6.4. But the single-digit choice is still easier and causes less hesitation. Once you get used to MILs, most shooters arrive at a binary choice construct – if it’s .5, they either always dial up or down. So, the hesitation is usually eliminated in their habits quickly.
Now think of that “math” or choice under pressure – you are on a deer and feel the pressure; you are on the match clock and feel the pressure; or you are on the battlefield, and the pressure is immense.
Conclusion: MIL single-digit rounding is more comfortable and faster.
Ease of Dialing
Your buddy ranges a target and calls out a range and elevation dial to you – 430 yards, 7.31 MOA. Hopefully, he is not a jerk and rounds it for you, lol – 7.25. Your brain, no matter how practiced, still has to realize you are dialing to 7 and one click more. That is an opportunity for mental hesitation and distraction.
For MILs, your buddy calls out 430 yards, 2.13 MILs (yes, he’s a jerk), you immediately disregard the “3” and dial 2.1. More likely, he called 2.1. You dial exactly what he called on your turret, 2.1. You don’t have to remember .25 is one click. If he calls 2.6, you dial 2.6, etc.
Conclusion: Dialing MILs is just simpler.

MIL Range Symmetry
Between 0 – 350 yards, neither MOA nor MIL have an easy symmetry to the range of the target. But at about 400 yards – 800 yards, a symmetry emerges with MILS that is not available in MOA. For most common cartridges, between about 350 and 850 yards, for every 10 yards in additional range, you add .1 MIL elevation.
Take a look at the chart below for information useful for the debate between MIL and MOA. It shows the 2-decimal ballistic solution output for both MOA and MIL. Next to that is the solution rounded to a dialable solution – .25 increments for MOA and .1 increments for MIL. Notice that for MILS (far right column) once you are at about 300 yards – for every 10 yards, it is a .1 increment to the next 10 yards – and for this 140-grain 6.5 Creedmoor solution that holds true all the way to about 900 yards.
| Range YDS | (MOA) | Rounded | Change | (MIL) | Rounded | Change | Change Speed Dope |
| 300 | 3.67 | 3.75 | 0.25 | 1.07 | 1.1 | 0.1 | – |
| 310 | 3.93 | 4.00 | 0.25 | 1.14 | 1.1 | 0.1 | – |
| 320 | 4.19 | 4.25 | 0.25 | 1.22 | 1.2 | 0.1 | – |
| 330 | 4.46 | 4.50 | 0.25 | 1.30 | 1.3 | 0.1 | – |
| 340 | 4.73 | 4.75 | 0.25 | 1.38 | 1.4 | 0.1 | – |
| 350 | 5.00 | 5.00 | 0.25 | 1.46 | 1.5 | 0.1 | 2.0 |
| 360 | 5.28 | 5.25 | 0.25 | 1.54 | 1.5 | 0.1 | 2.1 |
| 370 | 5.56 | 5.50 | 0.25 | 1.62 | 1.6 | 0.1 | 2.1 |
| 380 | 5.84 | 5.75 | 0.25 | 1.70 | 1.7 | 0.1 | 2.1 |
| 390 | 6.13 | 6.25 | 0.50 | 1.78 | 1.8 | 0.1 | 2.1 |
| 400 | 6.42 | 6.50 | 0.25 | 1.87 | 1.9 | 0.1 | 2.1 |
| 410 | 6.71 | 6.75 | 0.25 | 1.95 | 2.0 | 0.1 | 2.2 |
| 420 | 7.01 | 7.00 | 0.25 | 2.04 | 2.0 | 0.1 | 2.2 |
| 430 | 7.31 | 7.25 | 0.25 | 2.13 | 2.1 | 0.1 | 2.2 |
| 440 | 7.61 | 7.50 | 0.25 | 2.21 | 2.2 | 0.1 | 2.2 |
| 450 | 7.92 | 8.00 | 0.50 | 2.30 | 2.3 | 0.1 | 2.2 |
| 460 | 8.23 | 8.25 | 0.25 | 2.39 | 2.4 | 0.1 | 2.2 |
| 470 | 8.54 | 8.50 | 0.25 | 2.48 | 2.5 | 0.1 | 2.2 |
| 480 | 8.85 | 8.75 | 0.25 | 2.57 | 2.6 | 0.1 | 2.2 |
| 490 | 9.17 | 9.25 | 0.50 | 2.67 | 2.7 | 0.1 | 2.2 |
| 500 | 9.49 | 9.50 | 0.25 | 2.76 | 2.8 | 0.1 | 2.2 |
| 510 | 9.82 | 9.75 | 0.25 | 2.86 | 2.9 | 0.1 | 2.2 |
| 520 | 10.14 | 10.25 | 0.50 | 2.95 | 3.0 | 0.1 | 2.3 |
| 530 | 10.47 | 10.50 | 0.25 | 3.05 | 3.1 | 0.1 | 2.3 |
| 540 | 10.81 | 10.75 | 0.25 | 3.14 | 3.1 | 0.1 | 2.3 |
| 550 | 11.15 | 11.25 | 0.50 | 3.24 | 3.2 | 0.1 | 2.3 |
| 560 | 11.49 | 11.50 | 0.25 | 3.34 | 3.3 | 0.1 | 2.3 |
| 570 | 11.83 | 11.75 | 0.25 | 3.44 | 3.4 | 0.1 | 2.3 |
| 580 | 12.18 | 12.25 | 0.50 | 3.54 | 3.5 | 0.1 | 2.3 |
| 590 | 12.53 | 12.50 | 0.25 | 3.64 | 3.6 | 0.1 | 2.3 |
| 600 | 12.88 | 13.00 | 0.50 | 3.75 | 3.8 | 0.1 | 2.3 |
| 610 | 13.24 | 13.25 | 0.25 | 3.85 | 3.9 | 0.1 | 2.3 |
| 620 | 13.6 | 13.50 | 0.25 | 3.96 | 4.0 | 0.1 | 2.2 |
| 630 | 13.96 | 14.00 | 0.50 | 4.06 | 4.1 | 0.1 | 2.2 |
| 640 | 14.33 | 14.25 | 0.25 | 4.17 | 4.2 | 0.1 | 2.2 |
| 650 | 14.7 | 14.75 | 0.50 | 4.28 | 4.3 | 0.1 | 2.2 |
| 660 | 15.07 | 15.00 | 0.25 | 4.38 | 4.4 | 0.1 | 2.2 |
| 670 | 15.45 | 15.50 | 0.50 | 4.49 | 4.5 | 0.1 | 2.2 |
| 680 | 15.83 | 15.75 | 0.25 | 4.60 | 4.6 | 0.1 | 2.2 |
| 690 | 16.21 | 16.25 | 0.50 | 4.72 | 4.7 | 0.1 | 2.2 |
| 700 | 16.6 | 16.50 | 0.25 | 4.83 | 4.8 | 0.1 | 2.2 |
| 710 | 16.99 | 17.00 | 0.50 | 4.94 | 4.9 | 0.1 | 2.2 |
| 720 | 17.39 | 17.50 | 0.50 | 5.06 | 5.1 | 0.1 | 2.1 |
| 730 | 17.79 | 17.75 | 0.25 | 5.17 | 5.2 | 0.1 | 2.1 |
| 740 | 18.19 | 18.25 | 0.50 | 5.29 | 5.3 | 0.1 | 2.1 |
| 750 | 18.6 | 18.50 | 0.25 | 5.41 | 5.4 | 0.1 | 2.1 |
| 760 | 19.01 | 19.00 | 0.50 | 5.53 | 5.5 | 0.1 | 2.1 |
| 770 | 19.42 | 19.50 | 0.50 | 5.65 | 5.7 | 0.1 | 2.1 |
| 780 | 19.84 | 19.75 | 0.25 | 5.77 | 5.8 | 0.1 | 2.0 |
| 790 | 20.26 | 20.25 | 0.50 | 5.89 | 5.9 | 0.1 | 2.0 |
| 800 | 20.69 | 20.75 | 0.50 | 6.02 | 6.0 | 0.1 | 2.0 |
| 810 | 21.12 | 21.00 | 0.25 | 6.14 | 6.1 | 0.1 | 2.0 |
| 820 | 21.55 | 21.50 | 0.50 | 6.27 | 6.3 | 0.1 | 1.9 |
| 830 | 21.99 | 22.00 | 0.50 | 6.40 | 6.4 | 0.1 | 1.9 |
| 840 | 22.43 | 22.50 | 0.50 | 6.53 | 6.5 | 0.1 | 1.9 |
| 850 | 22.88 | 23.00 | 0.50 | 6.66 | 6.7 | 0.1 | 1.8 |
| 860 | 23.33 | 23.25 | 0.25 | 6.79 | 6.8 | 0.1 | 1.8 |
| 870 | 23.79 | 23.75 | 0.50 | 6.92 | 6.9 | 0.1 | 1.8 |
| 880 | 24.25 | 24.25 | 0.50 | 7.05 | 7.1 | 0.1 | 1.8 |
| 890 | 24.71 | 24.75 | 0.50 | 7.19 | 7.2 | 0.1 | 1.7 |
| 900 | 25.18 | 25.25 | 0.50 | 7.32 | 7.3 | 0.1 | 1.7 |
| 910 | 25.65 | 25.75 | 0.50 | 7.46 | 7.5 | 0.1 | 1.6 |
| 920 | 26.13 | 26.25 | 0.50 | 7.60 | 7.6 | 0.1 | 1.6 |
| 930 | 26.61 | 26.50 | 0.25 | 7.74 | 7.7 | 0.1 | 1.6 |
| 940 | 27.1 | 27.00 | 0.50 | 7.88 | 7.9 | 0.1 | 1.5 |
| 950 | 27.59 | 27.50 | 0.50 | 8.03 | 8.0 | 0.1 | 1.5 |
| 960 | 28.09 | 28.00 | 0.50 | 8.17 | 8.2 | 0.1 | 1.4 |
| 970 | 28.59 | 28.50 | 0.50 | 8.32 | 8.3 | 0.2 | 1.4 |
| 980 | 29.1 | 29.00 | 0.50 | 8.46 | 8.5 | 0.1 | 1.3 |
| 990 | 29.61 | 29.50 | 0.50 | 8.61 | 8.6 | 0.1 | 1.3 |
| 1000 | 30.13 | 30.25 | 0.75 | 8.76 | 8.8 | 0.2 | 1.2 |
It is true that due to rounding you may get the same “3.1” solution for 530 yds and 540 yds, but the real 2 decimal spread between those two solutions (3.05 and 3.14) is still closer to a .1 difference than not.
Look at the MOA column. The variance between ranges is almost a random order of .25 and .50 increments at various ranges.
So, working with making quick elevation adjustments from one range to the next within 100 yards of the original known range is pretty easy in MILS. For example, known range to target 1 is 610 yards, solution equals 3.9, target 2 emerges at an estimated range of 650 yards, you can simply dial up the .4 for the 40-yard distance to 4.3. You might be off by .1, but you are in the ballpark and able to do the math quickly in your head.
Conclusion: MILS align to range much simpler than MOA.
Speed Dope
Given the near-linear MIL symmetry above, there is a “Speed Dope” available to MIL users that is not available to MOA users its hard to compare use in the debate between MIL and MOA because Mil just wins. If you look at the chart above, you could manually derive a relationship between the yardage and an acceptable level of accuracy for determining a MIL solution. So, in the chart above, take 570 yards, solution = 3.4. Stay with me here – convert 570 to a number similar to the solution = 5.7 —- subtract 3.4 from 5.7 = 2.3. The yardage converted to a decimal number minus 2.3 equals the MIL solution between 520 and 610 yards. If I am willing to accept my dope being off by +/- .1, then we could use 2.2 as the Speed Dope factor, and then this method works between 360 and 770.
There is no such function in MOA – and if there theoretically a way to make it work, the brainpower required is beyond reasonableness under pressure and time constraints.
Conclusion: Speed Dope is available in MILs, but not MOA.
MILS are the KING of Wind
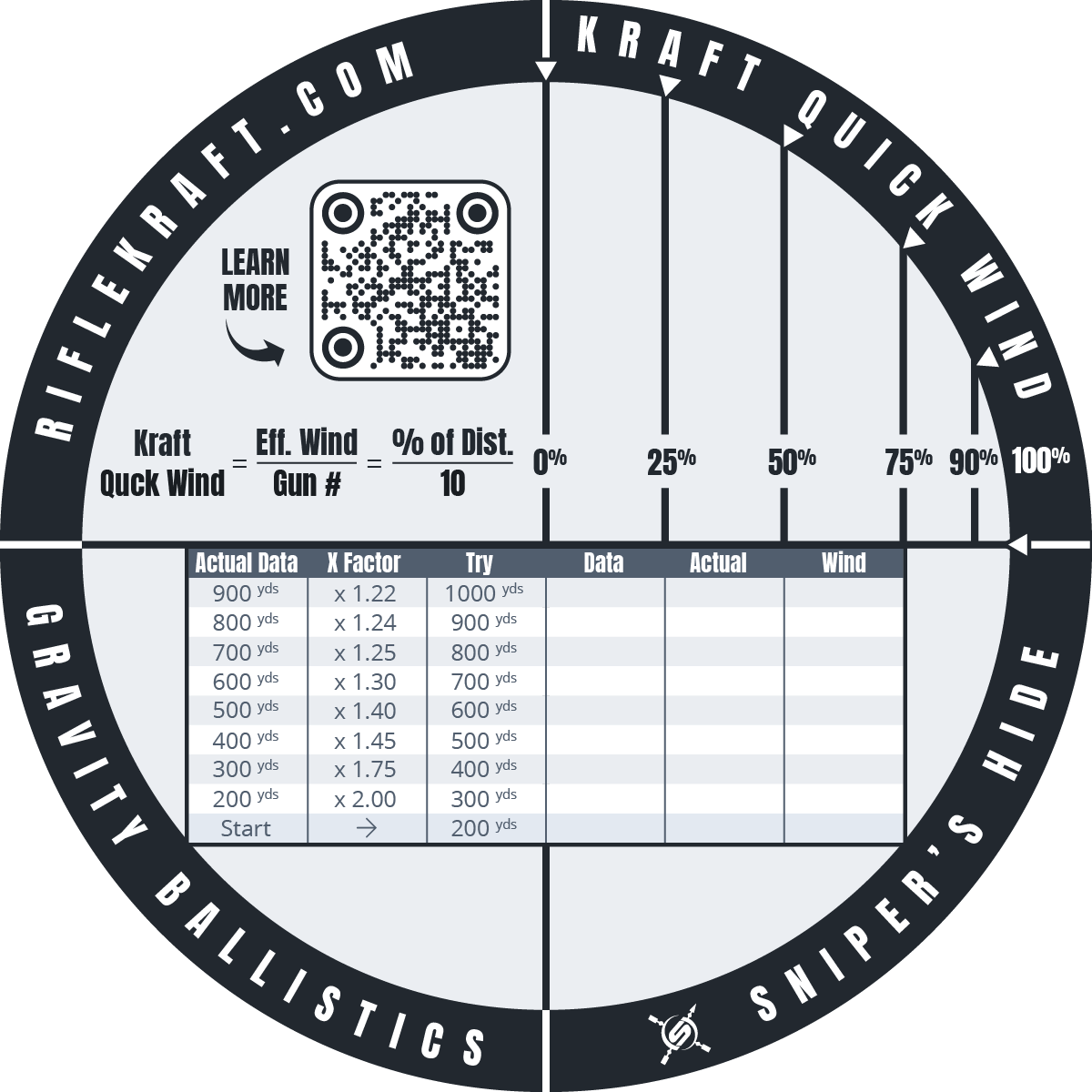
And now we come to the real Coup de Grace in the debate between MIL and MOA – WIND.
With MILs, you can work out a wind speed at which a full value wind (coming at a 90-degree angle to your shooting direction – often referred to as 3:00 o’clock or 9:00 o’clock wind – and not factoring in spin drift) will cause .6 mil of bullet drift at 600 yards (a .6 wind hold). Whatever wind speed that is for your caliber/ballistics is referred to as your “Gun Number” or “Wind Speed Number.” Therefore, if a 5mph full-value wind creates a .6 hold at 600 yards, then your gun is a “5mph gun.”
If you look at the holds required at each 100-yard increment now from 100 to about 700, you will notice that it works out to .1 at 100, .2 at 200……. .5 at 500, etc. SUPER SIMPLE.
Why is this so powerful? Well, if you are in a 10-mph wind, what do you think your hold is at 500 yards? Hmm, 10 = 2×5, so 2 x .5 = 1.0. Okay, that was too easy. What if you are shooting 600 yards and the wind is 7 mph? That’s about 7mph is about 1.5 (a tad less) x 5mph, so 1.5 x .6 = .9 or just a tad less.
The exact math: 7 mph / 5mph gun = 1.4 factor 1.4 x .6 = .84 = “a tad less than .9”
The reality is that your odds of calling wind so perfectly that you can make reliable sub-10th wind calls is nearly zero. Wind influences on a bullet happen across the whole 600 yards of flight – and our ability to know that the “7 mph” wind you may measure with your Kestrel at your shooting location is perfectly consistent in speed and angle over that entire 600 yards is nearly impossible.
There is NO comparable system to make wind holds in MOA that easy to calculate. There are innumerable discussions of how to create some sort of methodology. But they are not nearly as easy and neat as the MIL system allows.
These guys are awesome and I totally appreciate the effort. But it’s just not as simple and neat. MOA Wind Math – Sniper’s Hide
Conclusion:
WIND in MILs is far easier than in MOA.
Your call – stick with tradition and comfort, or make a tiny effort to update yourself to the ease of MILs?


