Hi guys – During the Frank/Marc show in PA a few weeks back, we all found that, at range, our true dope was less than what the weaponized math predicted and that the delta between dope at increasing range was not incrementing up as we would expect. The dope kind of flattened out at range.
Now this is in central (maybe a bit western) PA and the shooting line is in the valley and once past about 600 yards, the range started to go quite steeply up the side of the valley.
Frank explained what we were seeing as being a result of our shooting uphill and he used a diagram something like this which seemed to make a lot of sense at the time. Looking at this, it seemed clear to us at the time that yeah, the horizontal distance is less so that’s less of an horizontal distance for gravity to effect the drop of the bullet hence why our dope was coming out less than expected (and yeah, I believe we can discount any impact of a greater loss of velocity from going uphill as that would increase our dope and not reduce it from expected as we found and as Frank explained).
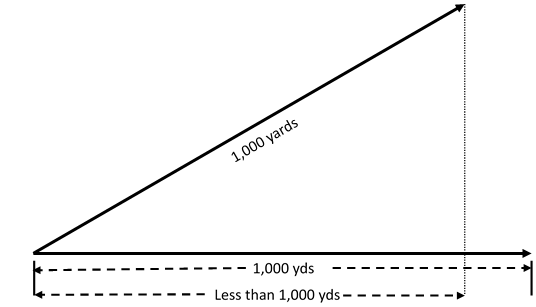
Now, I’m sure that Frank and Marc are right and I am not. And that this is why most good LRF will give you horizontal distance as well as slant range, if so chosen.
But as I thought about this more, I don’t understand why they are right (yeah, ole’ Baron23 asking why, why, why once again! haha).
The acceleration from gravity is defined as 9.8 m/s/s (9.8 meters per second per second, right). Note, there is nothing in here about horizontal distance. The absolute displacement resulting from this acceleration is purely a function of the time period that the bullet is exposed to gravity….that is, time of flight.
So, looking at the diagram above, I’d like to use a very simple example. 1,000 yard range target and a bullet going 3,000 fps (1,000 yds per second, right?). Also, for simplicity, let’s assume it’s a laser and there is no parabolic curve to the flight path and that the velocity remains constant across the time of flight.
So, a bullet shot purely in the horizontal will take 1 second to go 1,000 yards and the resulting drop will be 9.8 meters based on gravity accelerating the drop for 1 second.
Where I’m confused is that when shooting uphill the bullet also has a flight path of 1,000 yards to the target so it should also be exposed to the acceleration of gravity for 1 second and therefore the drop should be the same…i.e. 9.8 meters. But of course, it’s not.
Now, I’m really confident that Frank/Marc are correct and that there is a flaw in my thinking on this….but I don’t know what it is.
Any view on this…any explanation for why I’m wrong?
Now this is in central (maybe a bit western) PA and the shooting line is in the valley and once past about 600 yards, the range started to go quite steeply up the side of the valley.
Frank explained what we were seeing as being a result of our shooting uphill and he used a diagram something like this which seemed to make a lot of sense at the time. Looking at this, it seemed clear to us at the time that yeah, the horizontal distance is less so that’s less of an horizontal distance for gravity to effect the drop of the bullet hence why our dope was coming out less than expected (and yeah, I believe we can discount any impact of a greater loss of velocity from going uphill as that would increase our dope and not reduce it from expected as we found and as Frank explained).
Now, I’m sure that Frank and Marc are right and I am not. And that this is why most good LRF will give you horizontal distance as well as slant range, if so chosen.
But as I thought about this more, I don’t understand why they are right (yeah, ole’ Baron23 asking why, why, why once again! haha).
The acceleration from gravity is defined as 9.8 m/s/s (9.8 meters per second per second, right). Note, there is nothing in here about horizontal distance. The absolute displacement resulting from this acceleration is purely a function of the time period that the bullet is exposed to gravity….that is, time of flight.
So, looking at the diagram above, I’d like to use a very simple example. 1,000 yard range target and a bullet going 3,000 fps (1,000 yds per second, right?). Also, for simplicity, let’s assume it’s a laser and there is no parabolic curve to the flight path and that the velocity remains constant across the time of flight.
So, a bullet shot purely in the horizontal will take 1 second to go 1,000 yards and the resulting drop will be 9.8 meters based on gravity accelerating the drop for 1 second.
Where I’m confused is that when shooting uphill the bullet also has a flight path of 1,000 yards to the target so it should also be exposed to the acceleration of gravity for 1 second and therefore the drop should be the same…i.e. 9.8 meters. But of course, it’s not.
Now, I’m really confident that Frank/Marc are correct and that there is a flaw in my thinking on this….but I don’t know what it is.
Any view on this…any explanation for why I’m wrong?





