Haha….apparently not everybody agrees w us on that.
- Thread starter Baron23
- Start date
It's actually not quite that simple, because drop and wind drift have to be considered differently for inclined shots.
Drop is similar to (but not exactly the same as) the horizontal distance, we've been over that here, but for wind drift you have to use the actual measured distance because it's not a gravity issue, it's a time of flight & wind issue. No nerd stuff necessary, but it's worth understanding that the horizontal distance isn't correct for estimating wind. (Of course estimating wind is hard enough that maybe this doesn't matter most of the time anyway.)
Well, if I have learned anything from @Dthomas3523, it is I'll score more points if I think less about wind and more about the fundamentals of marksmanship and how to address building a solid position. Now, @Diver160651 says that I really don't need to think too much about the angle, as its only really important for extremely high angle shooting- and again focus on building a solid position. This long range shooting just keeps getting easier. As soon as someone says I don't have to think about range any more, and just focus on building a solid position, I will have this long range shooting thing licked. 
First, measure the true "slant range" R to your target, as you would using a rangefinder. Second, measure the slope angle THETA above or below the horizontal for your line-of-sight to that target.
Then calculate the total drop D from the axis of your bore when firing your rifle horizontally to range R. You can fake most ballistics programs into doing this by temporarily setting your scope height to 0.0 and your "zero distance" to 5 or 10 yards.
Now, calculate d = D*[1 - Cos(THETA)]. This distance d is how much you would shoot over the target using your drop and zeroing dope for range R. In hunting, you should just aim low by this distance d using "Kentucky elevation" and avoid shooting over the back of the animal. In target shooting, you can convert this distance d at range R into your scope's elevation clicks and dial in the adjustment. [This "1 - Cosine" function frequently arises in geometry and mechanics, and was named the "versine" function in ancient trigonometry.]
For practical purposes shooting uphill or downhill at slope THETA is symmetrical. Either way, your shot will impact a distance d too high without correction. The minor gravitational difference between the two cases is largely offset by the variation in air density (and drag force) at differing heights above mean sea level, at least for moderate slope angles THETA. Shooting uphill, the rifle bullet experiences some extra gravitational retardation, but it is travelling through progressively thinner air (and vice versa).
Then calculate the total drop D from the axis of your bore when firing your rifle horizontally to range R. You can fake most ballistics programs into doing this by temporarily setting your scope height to 0.0 and your "zero distance" to 5 or 10 yards.
Now, calculate d = D*[1 - Cos(THETA)]. This distance d is how much you would shoot over the target using your drop and zeroing dope for range R. In hunting, you should just aim low by this distance d using "Kentucky elevation" and avoid shooting over the back of the animal. In target shooting, you can convert this distance d at range R into your scope's elevation clicks and dial in the adjustment. [This "1 - Cosine" function frequently arises in geometry and mechanics, and was named the "versine" function in ancient trigonometry.]
For practical purposes shooting uphill or downhill at slope THETA is symmetrical. Either way, your shot will impact a distance d too high without correction. The minor gravitational difference between the two cases is largely offset by the variation in air density (and drag force) at differing heights above mean sea level, at least for moderate slope angles THETA. Shooting uphill, the rifle bullet experiences some extra gravitational retardation, but it is travelling through progressively thinner air (and vice versa).
Last edited:
Overheard at the next PRS event.
“Hey, wha happened? You normally shoot better.”
“Yeah, it’s my bullets. They’re gravitationally retarded.”
“Hey, wha happened? You normally shoot better.”
“Yeah, it’s my bullets. They’re gravitationally retarded.”
Haha. Frank said in the Marines that when shooting uphill to aim for their balls and you’ll hit them somewhere.
He may have been joking but…..lol
Well since Gravity and Acceleration are equivalent in general relativity, maybe I should calculate the time dilation the bullet experiences as it accelerates....
I haven't reread the whole thread in depth, but the basics as I understand it is, gravity affects bullet drop over distance (and time). The shorter the time to target (which is related to horizontal distance to target and velocity), the less gravity affects the bullet.
As Marge Simpson said to John the Gay Antiques Dealer, when he told her, "Helen Lovejoy? She may look blonde, but I've heard cuffs and collar don't match - if you catch my drift ...":
"I don't ... but I loved hearing it."
I don't understand half of what's in this thread, and not sure I ever will ... but glad there's people out there who do.
All I really need to do is to remember what this does for my dope ... I think.
Who's with me?
"I don't ... but I loved hearing it."
I don't understand half of what's in this thread, and not sure I ever will ... but glad there's people out there who do.
All I really need to do is to remember what this does for my dope ... I think.
Who's with me?
If there is any take away, it is not to sweat the angle too much. By the time you are at sufficient angle that it really matters, you will KNOW that you need to account for that angle.As Marge Simpson said to John the Gay Antiques Dealer, when he told her, "Helen Lovejoy? She may look blonde, but I've heard cuffs and collar don't match - if you catch my drift ...":
"I don't ... but I loved hearing it."
I don't understand half of what's in this thread, and not sure I ever will ... but glad there's people out there who do.
All I really need to do is to remember what this does for my dope ... I think.
Who's with me?
147g 6.5mm ELD-M at 2700 fps. 100 yard zero. Sea level.
hehehe...yeah, Frank, right you are....but I'm retired and bored so....LOL
And it was fairly surprising to see how many different takes there are on the "why" of it all.
Cheers
Not everyone understands things here as well as they think they do, and not all of the answers you received are correct.
Sometimes the most complex explanations seem smart but are wrong because the person doesn’t understand it enough to give a simple answer. Just beware of what you trust.
One of the first solutions suggested is the old "rifleman's rule" which is only a first order approximation. It is no longer adequate for accurate modern rifles. My "total drop from bore axis times [1 - Cos(Theta)]" solution is physics based, but is not quite a full 6-degree of freedom integration from launch conditions.
Yup, that's where the 'improved' rules come from and they become harder and harder to approximate in your head.
If you look at the 'pure' rifleman rule (no drag) with R_s as the slant distance, R_H as the horizontal distance, alpha as the incline and s as your 'dope' or shooting angle
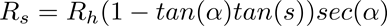
tan s tends to be VERY VERY small. I mean what's your typical dope? 10 mils say? 10 milliraidians? or 0.010 radians? tan s is then basically 0. so then the (tan a * tan s) becomes small and you get the 1st order approximate basic riflemans rule (sec a is just 1/cos a)
of course at high incline (large alpha) and long distnace (large s) this no longer holds and Jim says--we are shooting much longer distances and much smaller targets.
But even the improved dope * cos dope will get you to 1000 yards within 2 inches at 15 degrees. Its only at higher and higher angles this becomes an issue
Now I am not a mountain hunter, so i dunno about those guys incline, but I would thank the sharpest angles would be urban law enforcement--how many 400 yards shots 60 degrees do they take? This one seems pretty good for now. (plus it gets easy to aproximate cos in your head).
If you look at the 'pure' rifleman rule (no drag) with R_s as the slant distance, R_H as the horizontal distance, alpha as the incline and s as your 'dope' or shooting angle
tan s tends to be VERY VERY small. I mean what's your typical dope? 10 mils say? 10 milliraidians? or 0.010 radians? tan s is then basically 0. so then the (tan a * tan s) becomes small and you get the 1st order approximate basic riflemans rule (sec a is just 1/cos a)
of course at high incline (large alpha) and long distnace (large s) this no longer holds and Jim says--we are shooting much longer distances and much smaller targets.
But even the improved dope * cos dope will get you to 1000 yards within 2 inches at 15 degrees. Its only at higher and higher angles this becomes an issue
Now I am not a mountain hunter, so i dunno about those guys incline, but I would thank the sharpest angles would be urban law enforcement--how many 400 yards shots 60 degrees do they take? This one seems pretty good for now. (plus it gets easy to aproximate cos in your head).
Last edited:
Rifleman's rule is total crap.
"Improved" works way better, but depends on zero distance.
cf. https://geladen.ch/en/inclined-fire/
"Improved" works way better, but depends on zero distance.
cf. https://geladen.ch/en/inclined-fire/
Yeah but then we’d all have to argue whether it really made a difference or just helped with less case trimming.
I consulted with Ted Almgren and the late Bill McDonald of Sierra on their uphill/downhill shooting correction. I believe that my formulation is equivalent to theirs, but simpler in application. Slant Range (R) and slope angle (A) are directly measured in the field nowadays. A table of "total bullet DROP from bore axis for horizontal firing" can be printed out ahead of time for the selected shooting equipment and the expected shooting conditions using Sierra Infinity, or any similar point-mass trajectory propagator. [Just temporarily set scope height to 0.0 and Zero Range to 5 or 10 yards or meters.] A pocket calculator can be used to interpolate the total DROP table values at the measured slant range R. My calculator can calculate the cosine of the slope angle A, so I would simply multiply the DROP*[1 - COS(A)] to find the overshoot distance (d) at the target. By applying of the Rigid Trajectory Theory over this small correction angle (d/R in radians), that overshoot distance is inherently perpendicular to your line-of-sight to the target, so dividing d*1000 by the slant range R to that target directly yields the (lower) aiming correction CORR in "milliradians (MILs)." A minute of angle (MOA) is 1/(360*60) of a full circle which is also 2000*Pi milliradians, so the conversion factor is 360*60/(2000*Pi) = 3.43775 MOA/MIL. [Write that conversion factor down and store it in your calculator if your scope adjustments are made in MOA.]
This formulation is based upon the fact that the gravity gradient is perpendicular to your line-of-sight throughout the bullet's flight to the target only when firing with the bore absolutely horizontal. I call this the total bullet DROP from the bore axis to the horizontal target range R. If the gravity gradient were hypothetically reduced all along the flight path of the bullet by a factor of [1 - COS(A)] as when firing uphill or downhill at slope A, the drop from the bore axis will be reduced by that same proportion [1 - COS(A)], with the air drag effects being the same in both cases. I reason that if you know how to hit a horizontally distant target with this equipment in these shooting conditions at a horizontal range R, then your point of impact would be high by about the correction distance d when shooting uphill or downhill with your line-of-sight sloping at a (positive of negative) angle A when using your best shooting "dope" for that horizontal range R. I say "about the same overshoot distance d" because the uphill and downhill cases are not quite identically symmetric due to the along-the-line-of-sight gravity force components acting on the bullet, but working in opposite directions. However, after considering the systematic differences in air-drag experienced by the two bullets along their two different trajectories, these differences in overshoot distance d are negligible in practical shooting.
This formulation is based upon the fact that the gravity gradient is perpendicular to your line-of-sight throughout the bullet's flight to the target only when firing with the bore absolutely horizontal. I call this the total bullet DROP from the bore axis to the horizontal target range R. If the gravity gradient were hypothetically reduced all along the flight path of the bullet by a factor of [1 - COS(A)] as when firing uphill or downhill at slope A, the drop from the bore axis will be reduced by that same proportion [1 - COS(A)], with the air drag effects being the same in both cases. I reason that if you know how to hit a horizontally distant target with this equipment in these shooting conditions at a horizontal range R, then your point of impact would be high by about the correction distance d when shooting uphill or downhill with your line-of-sight sloping at a (positive of negative) angle A when using your best shooting "dope" for that horizontal range R. I say "about the same overshoot distance d" because the uphill and downhill cases are not quite identically symmetric due to the along-the-line-of-sight gravity force components acting on the bullet, but working in opposite directions. However, after considering the systematic differences in air-drag experienced by the two bullets along their two different trajectories, these differences in overshoot distance d are negligible in practical shooting.
You should try reading your own posts, and ask yourself if they sound like simple explanations or solutions. Even as an engineer who’s used to reading technical documents, your stuff is pretty hard to read.
If you want to reach the average long range shooter, you have to simplify your explanations and make the solution something that’s actually useful in the field.
If I have to carry a calculator (I.e. a smartphone these days) to solve this, I might as well just consult a ballistic app that can get closer anyway. The link ptosis posted above has about the only workable paper solution I’ve seen that’s good for longer distances.
I apologize for using too many big words, but the concept seems quite simple to me. It is another implementation of exactly the Sierra calculation which ptosis admired along with a simple physical explanation of how it works.
As far as battery-free solution go, nowadays I just put the angle of sight adjustments directly in the rangecards, e.g. https://k31.ch/wp-content/uploads/2021/10/rangecards-k31-xxi-easy-v7.pdf
Improved rifleman's (eventually with the EBRR clicks) is ok for an occasional shot. But if the angle of sight adjustment has to be done for every target (which is often the case where I shoot), it quickly gets tedious and prone to errors.
Improved rifleman's (eventually with the EBRR clicks) is ok for an occasional shot. But if the angle of sight adjustment has to be done for every target (which is often the case where I shoot), it quickly gets tedious and prone to errors.
I think this perfectly illustrates the need for multiple rules.
If you are the avg hunter--the riflemans rule is perfectly fine
If you hunt out west or are a precision competitor--the improved rules becomes your friend
If are doing ELR or extremem precision, the ballistic calcs are what are needed.
People become obssesed with precision (and not just the rifle kind). Its important to know what kind of precision you need. I don't need modern calculus to solve 7-5. I just memorize it.
Often times I approximate pi as 3 because it is a ton faster and easier to multiple by 3 than 3.14, (or go old school and use 22/7)
And and some point (its around 5 decimal places) the more and more precision values of pi become an academic exercise.
Its important to know the 'rules' or approximations and where they break down and the 'cost' of improved calculations.
But on the otherhand, if someone does have a very technical explantion of something, but it can't be boild down--its still valid. Modern Quantum Electrodynamics can not be boiled down, but it has useful applications. BUt its also overkill for the average hunter.
What precision do you need?
What gets you there?
Yes you can have pre-printed dope cards--but at what angles are you printing cards? every degree, every five degrees? Even then you have to put in a cutoff somewhere.
If it works--go with it.
If it doesn't work, find something that works and go with it.
If you are the avg hunter--the riflemans rule is perfectly fine
If you hunt out west or are a precision competitor--the improved rules becomes your friend
If are doing ELR or extremem precision, the ballistic calcs are what are needed.
People become obssesed with precision (and not just the rifle kind). Its important to know what kind of precision you need. I don't need modern calculus to solve 7-5. I just memorize it.
Often times I approximate pi as 3 because it is a ton faster and easier to multiple by 3 than 3.14, (or go old school and use 22/7)
And and some point (its around 5 decimal places) the more and more precision values of pi become an academic exercise.
Its important to know the 'rules' or approximations and where they break down and the 'cost' of improved calculations.
But on the otherhand, if someone does have a very technical explantion of something, but it can't be boild down--its still valid. Modern Quantum Electrodynamics can not be boiled down, but it has useful applications. BUt its also overkill for the average hunter.
What precision do you need?
What gets you there?
Yes you can have pre-printed dope cards--but at what angles are you printing cards? every degree, every five degrees? Even then you have to put in a cutoff somewhere.
If it works--go with it.
If it doesn't work, find something that works and go with it.
A kestrel is the gold standard calculator (5700 level). (Everyone gets measured against it)
The "Improved Rifleman's rule" is the "in your head" standard.
The true gold standard is your DOPE
The "Improved Rifleman's rule" is the "in your head" standard.
The true gold standard is your DOPE
A Kestrel 5700 and a Vectronix PLRF. Cool.
1. Any smaprtphone with Android or iOS, and the ballistic calculator app which has the user interface that you like best (they all do the same, to a rounding error close). My personal preference goes to calculators which understand and use publicly available Doppler-measured curves -- Lapua 6DOF and Strelok Pro.
2. Pen and paper, until you get to the ballistic card format, which suits best your shooting requirement, as @DocRDS has put it -- "What precision do you need? What gets you there?" -- and especially, if I may add, a specific attention to discarding what is not important in getting you there.
Some of you guys really need to go shoot 600+ yards at 30-45 degrees and report back what you find.
Here's what I've found:
1. Most people here will have a difficult time finding a suitable spot that offers such conditions due to the angle of repose of most soils and weathering of edges to shoot from.
2. Most people will find a 30-45 angle ridiculous enough that they can not shoot well.
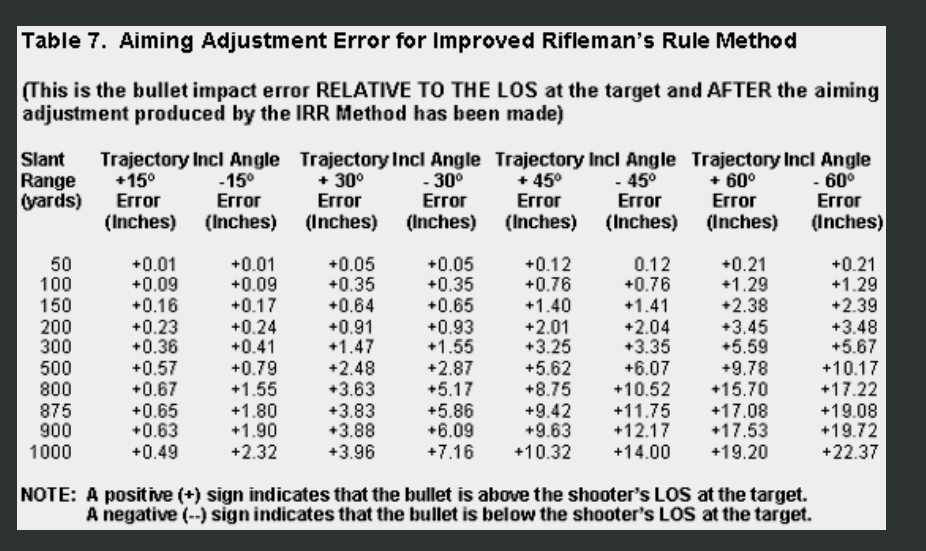
Food for thought, the lowest number on the chart posted is -/+ 15 degrees only providing a 2-3" offset @ 1,000 yards. In context, that means you are having to shoot over 800 vertical feet at 1,000y -- at 45, you're need to shoot a crazy 3,000 foot vertical.
Here's what I've found:
1. Most people here will have a difficult time finding a suitable spot that offers such conditions due to the angle of repose of most soils and weathering of edges to shoot from.
2. Most people will find a 30-45 angle ridiculous enough that they can not shoot well.
Food for thought, the lowest number on the chart posted is -/+ 15 degrees only providing a 2-3" offset @ 1,000 yards. In context, that means you are having to shoot over 800 vertical feet at 1,000y -- at 45, you're need to shoot a crazy 3,000 foot vertical.
I missed a shot on a 600 yard target once, that happened to be very close to 30 degrees inclined but it didn't seem like that much. Took me a second to realize why I was hitting high. That was shooting off the edge of a bluff down in central Oregon (that particular area has some bluffs similar to New Mexico or other parts of the west, where angles can be large). IIRC I was hitting 0.5 mil high, shooting 6.5 Creed, although my memory is fuzzy on the exact amount high and I don't have my stuff handy to confirm.
Just FWIW. It does happen.
+1. In [pretty extreme] alpine terrain, most shots do not exceed ±20° LoS elevation. If I remember well, the steepest shot I ever had to take was -33°.
LOL.
Similar threads
Advanced Marksmanship Formula for correcting Elevation on misses
