Just want to thank the hide members for their feedback to me. Very little has been meaningful and most has been comical: I hope y’all learn something from testing that incorporates statistical significance testing. https://youtube.com/@WitchDoctorPrecision?si=oNVYHOH0y6POeFj8
Join the Hide community
Get access to live stream, lessons, the post exchange, and chat with other snipers.
Register
Download Gravity Ballistics
Get help to accurately calculate and scope your sniper rifle using real shooting data.

Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Great feedback from “the hide” members
- Thread starter Sniper King 2020
- Start date
If anything, the plug for the YouTube channel would get more attention in The Pit.Wrong section.
Damn, sometimes I just love this place. . .
Link can’t seem to open because I won’t give you a view..
Is it a video of you announcing that you’re getting ribs removed so you can suck yourself off?
Is it a video of you announcing that you’re getting ribs removed so you can suck yourself off?
I feel like this belongs in the Bear Pit. That way we can test the meaningful statistical significance of all the fantastic memes and gifs we are about to witness.
His point of contention was Garmin used STDEV.P while other chronographs use STDEV.S. He tried telling everyone that STDEV.P is the correct format. Even tried flexing his credentials to do so, until an actual statistician said no, you're shooting samples of a population, and almost never shoot a full population. Cry ensued.
PM sent
I already know that you two are going to have a great discussion about how mean the forum is that you make a conscious choice to be on
I'd personally love to hear your opinion on STDEV.P and STDEV.S as pertaining to ammunition velocity.
STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
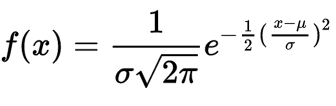
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
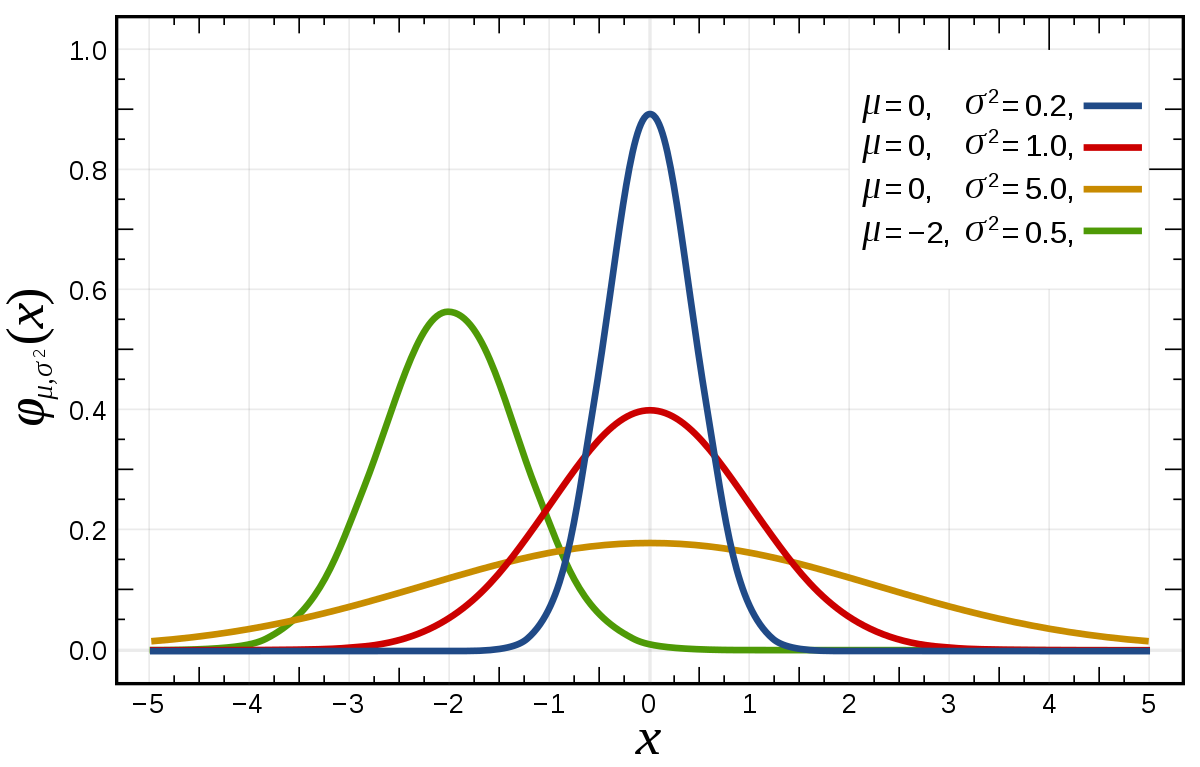
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"

 colab.research.google.com
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
colab.research.google.com
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
Google Colab
[FONT=courier new]import numpy as np
p=[]
s=[]
n=10
size=5
for i in range( n ):
x =np.random.normal(loc=2800, scale=10.0, size=size)
p.append(np.std(x))
tmp = (x-x.mean())**2
tmp = tmp.sum()
tmp = 1/(size-1) * tmp
tmp = np.sqrt(tmp)
s.append(tmp)
import matplotlib.pyplot as plt
plt.scatter(np.linspace(0,9,10),p,label="True")
plt.scatter(np.linspace(0,9,10),s,label="Estimated")
plt.legend()
plt.show()
sigma=[]
for i in range(100):
tmp = np.random.choice(x,5,replace=True)
print(tmp)
sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4))
print(np.percentile(sigma,95))
print(np.percentile(sigma,5))
print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
Last edited:
STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]

STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
Thanks for reply. This echos just about the same from everyone I've asked. He was so insistent he was correct that I looked to anything or anyone who might be on the same side of the coin and explain it.
Thus far, he's the only one who agrees with his assertion.
STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
I was gonna post every single thing here, but you beat me to it…STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
I’m truly curious to see if @Bryan Zolnikov will respond to @DocRDS. That will show that he is serious and actually is willing to discuss this intelligently or is just simpering for his fans.
ETA:
I had to edit this to reference the OPs new name, which is now @Sniper King 2020.
How about it Mr. King. Are you going to respond to or at least acknowledge the serious and reasonable responses to your question in the post that started this thread? Or was that just a troll post? Inquiring minds need to know.
My personal money is on that he’s trolling for clicks on his utoob posts for income generation. Not today Satan, not today.
ETA:
I had to edit this to reference the OPs new name, which is now @Sniper King 2020.
How about it Mr. King. Are you going to respond to or at least acknowledge the serious and reasonable responses to your question in the post that started this thread? Or was that just a troll post? Inquiring minds need to know.
My personal money is on that he’s trolling for clicks on his utoob posts for income generation. Not today Satan, not today.
Last edited:
He's saving up his liquid courage and won't be back for a few days, but I assure you when he does, there will be a meltdown of galactic proportions, if recent history is any indication.I’m truly curious to see if @Bryan Zolnikov will respond to @DocRDS. That will show that he is serious and actually is willing to discuss this intelligently or is just simpering for his fans.
Probably not because he used the term "inflated" when taking about the Labradar vs Garmin. The correct term in "unbiased" When sampling from a distribution your are biasing your measurements. The STDEV.S method is an attempt to "unbias" the measurement of std deviation.
The point being, somebody looked at the formula in Excel, but didn't understand why they were different or have a deep understanding of concave functions
Don't take my word for it--NIST agrees with me (and apparently everyone else):
And I thought I had the semester off from teaching...
The point being, somebody looked at the formula in Excel, but didn't understand why they were different or have a deep understanding of concave functions
Don't take my word for it--NIST agrees with me (and apparently everyone else):
7.3.1. Do two processes have the same mean?
www.itl.nist.gov
And I thought I had the semester off from teaching...
Now, what if we wanted to use Bayesian statistics?STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
I’m truly curious to see if @Bryan Zolnikov will respond to @DocRDS. That will show that he is serious and actually is willing to discuss this intelligently or is just simpering for his fans.
He didn't even acknowledge @JB.IC last time. Who also has a higher eduction on the subject.
Which is pretty entertaining since he was so fast to cite his own education as the reason he was right (rather than explaining why). Then totally ignores people with more education than he has.
Now, what if we wanted to use Bayesian statistics?
Chapter 16 Comparing Two Samples | An Introduction to Bayesian Reasoning and Methods
This textbook presents an introduction to Bayesian reasoning and methods
bookdown.org
Also calling it now: I technically don't have a math degree--I have a physics degree (couple of em).
I only TEACH data science and statistics at a D1 school.
STDEV.S is the correct method. End of story.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
I’m a math idiot and a howler monkey. So, “HOO HOO HOO HOOOOOOWWWLLL!!!” to you, pal!I'm, not getting into psuedo-random numbers with howler monkies.
I also witnessed time & space warp in the initial Byran thread and became actually, uh, concerned for the guy. So this is not a defense of anything he has ever said (or will say lol).
PART I
I am going to say back to you what I think you said, only in howler monkey. Please tell me if I’m on track.STDEV.S is like taking a sample out of the ocean. Measuring what? Doesn’t matter. You know there is a lot more ocean water out there, so all you can do is estimate is via the small sample you took.
STDEV.P is…what? Like you created some cookies and ran tests on ALL of the cookies? Your tests tell you mostly everything about your existing cookies, but can tell you little-to-nothing about the next batch you make?
PART II
The following question assumes that Labradar and Magnetospeed use STDEV.S, which Mr. Byran said they do (in a deleted thread, I believe, and also in one of his vids that I didn’t watch).If STDEV.S is the correct method, why do you think Garmin chose STDEV.P? (Mr. Byran said that too, that Garmin uses STDEV.P).
Edit: you might be saying Byran didn’t understand how these chronos calculate SD…so my question might be totally off base. “HO HOO HO HOOOO!”
******
Please speak in one-to-two syllable words, like you’re explaining this to a ten year-old.
Check that.
To a ten year-old howler monkey. Lol
Last edited:
That's the thing about the Hide. You never know when you're talking to an actual expert, and the chances are pretty high. Like when a new member here posted a while back about where KAC sourced their parts. He was corrected, then doubled downed, not knowing that he was talking to a member of the senior management at Knight's.
You got it pretty straight.I’m a math idiot and a howler monkey. So, “HOO HOO HOO HOOOOOOWWWLLL!!!” to you, pal!
I also witnessed time & space warp in the initial Byran thread and became actually, uh, concerned for the guy. So this is not a defense of anything he has ever said (or will say lol).
PART I
I am going to say back to you what I think you said, only in howler monkey. Please tell me if I’m on track.
STDEV.S is like taking a sample out of the ocean. Measuring what? Doesn’t matter. You know there is a lot more ocean water out there, so all you can do is estimate is via the small sample you took.
STDEV.P is…what? Like you created some cookies and ran tests on ALL of the cookies? Your tests tell you mostly everything about your existing cookies, but can tell you little-to-nothing about the next batch you make?
PART II
The following question assumes that Labradar and Magnetospeed use STDEV.S, which Mr. Byran said they do (in a deleted thread, I believe, and also in one of his vids that I didn’t watch).
If STDEV.S is the correct method, why do you think Garmin chose STDEV.P? (Mr. Byran said that too, that Garmin uses STDEV.P).
******
Please speak in one-to-two syllable words, like you’re explaining this to a ten year-old.
Check that.
To a ten year-old howler monkey. Lol
Part ii: Its only when I'm really pissed off that I say people do things wrong, I would have gone with the "unbiased" method, but since you have the data, you can always just calculate it yourself. Also as you take larger samples, the two converge (aka become the same). Just now the garmin produces a "biased" (aka lower) std dev given the same inputs. Literally the difference is Garmin divides by 1/N while LR divides by 1/(N-1). (inside a square root). So you have "correct" the Garmin by multipling the result by SQRT(N/N-1) which for N= 5 is about 10% more (approximately because the physics guy in me likes easy math)
Now for the howler monkey because I'm kinda enjoying my flex (I try not, but sometimes):
There is no such thing as a random number in computer science. There you made me do it. Since computers are deterministic, you can always "reproduce" the randomness. SO if i hadn't been lazy I could have seeded the results, passed that seed onto you guys and then you would have gotten the exact same "random" results.
I do remember reading that somewhere. How do the science & math fields account for that? Or do they?There is no such thing as a random number in computer science.
I’ve always wondered if many huge glittering theories about the cosmos are underpinned by such assumptions that even very math-savvy people choose to ignore.
They ignore them because if they don’t, then problem becomes too complicated, too murky. Too…lifelike.
A large version of, “Ok class, in this equation we are going to discount friction.”
(Thx for the reply, btw!)
Last edited:
Bayes overfits data and have limited application of usefulness (I’m not saying Bayes is useless. I’m saying Bayes isn’t what they sold it to be). In fact, a tech company that hired a team Bayesian Statisticians fired all of them because their models were garbage.Now, what if we wanted to use Bayesian statistics?
The priors are picked with hardly any evidence to support their value. Then the priors are updated to fit the data through Frequentist approaches. Then the model overfits the data.
There has been big brain research statisticians argue how useless Bayes is and reality has mirrored it. The entire Data Science community moves like a flock of birds to the next best thing and Bayes has never been the next best thing.
There is no such thing as a random number in computer science.
Would you consider hardware generated random numbers separate? Or is there a way to still predict hardware generated numbers like it's possible with software generated?
In all practicality, software generated random numbers (pseudo random number generators) are sufficient for generating random numbers as a truly theoretical random. Reproducibility in science is important and pseudo random numbers ensure that reproducibility.Would you consider hardware generated random numbers separate? Or is there a way to still predict hardware generated numbers like it's possible with software generated?
LOL. Guess he figured out using his real name wasn't the wisest. Ol boy has a name change.
Holy crap!STDEV.S is the correct method. End of story.
The difference between the two (open google--cause statisticians don't use those terms, there is standard deviation (STDEV.P)--statisticians use sigma and then there is ESTIMATED standard deviation,(STDDEV.S) which is known a 's'.
Its like your measured values is "x" and the mean is "mu"
English variables mean "measured" and greek variables are "intrinsic"--properties of the distribution
Standard Deviation is the width on a Normal or Gaussian Distribution. The formula is:
View attachment 8323682
sigma is the Std Dev. mu (the u thingy) is the mean).
Its a complicated formula, but just know that sigma controls the width, and mu controls the location:
View attachment 8323683
That's pretty standard stuff, but that's pure THEORY (egads a running gag in my own posts). When you MEASURE something you are sampling from that theoretical distribution (you get points at random, from a random distribution). Assuming your distribution is normal (not always safe), you can estimate the TRUE Standard Deviation by using the Estimated Standard Deviation, s. They key here is there is some unknown TRUE sigma which we try and estimate by taking samples. The Estimated and True will only begin to approach equal once the number of samples becomes very very large.
So the TLDR version is STDEV.S would be the statistician's choice to ESTIMATE the standard deviation of your velocity.
Example: I ran created a distribution with mean 2800 and simga 10. I grabbed 5 samples at random, 10 times and took the STDEV.P--However, we KNOW its 10 (I made it!). Here are the results:
"True Method"
[13.275930373733024,
8.342655830573312,
7.23926247655942,
5.156843761443447,
8.550960467769086,
13.76093532000941,
3.2590625589140196,
7.783767404854264,
3.911747500033366,
7.031416934586289]
Estimated:
[14.842941390110614,
9.327372775023447,
8.09374150227517,
5.765526599966628,
9.560264439422538,
15.385193404759432,
3.6437427123280806,
8.702516519150631,
4.373466660444734,
7.861363121939068]
With the estimated std dev, you get a value that is higher (instead of dividing by num of samples, you divide by n-1 for math reasons--in reality using the "true" method induces a bias towards 0)--so you could get lucky or you could get unlucky.
OR
Based on the following random data I "sampled":
array([2794.70526224, 2816.48889134, 2797.31856425, 2785.55297754,
2791.62315356])
I would publish an s of 11.67 with 95% CI of (4.07, 14.80) meaning I am 95% sure the TRUE sigma lies on the interval 4.07 to 14.80
You use confidence intervals : since I have to publish shit for the dreaded peer review, I would say my estimated std dev is 10.4 (4.07, 14.80)
So I read that as a sample size of 5 means dick either way. But "s" is the correct method.
Also statisticians don't use excel, they use R, which is a filthy language.
I teach data science/AI so I use python:
Go to google colab and reproduce my results. I prob made a mistake, but I fuck it. That's how you think of this as a "statistician"
spaces are important in the code btw Due to RNG, your number may vary slightly from mine. I'm, not getting into psuedo-random numbers with howler monkies.
Google Colab
colab.research.google.com
[FONT=courier new]import numpy as np p=[] s=[] n=10 size=5 for i in range( n ): x =np.random.normal(loc=2800, scale=10.0, size=size) p.append(np.std(x)) tmp = (x-x.mean())**2 tmp = tmp.sum() tmp = 1/(size-1) * tmp tmp = np.sqrt(tmp) s.append(tmp) import matplotlib.pyplot as plt plt.scatter(np.linspace(0,9,10),p,label="True") plt.scatter(np.linspace(0,9,10),s,label="Estimated") plt.legend() plt.show() sigma=[] for i in range(100): tmp = np.random.choice(x,5,replace=True) print(tmp) sigma.append(np.sqrt((((tmp-tmp.mean())**2).sum())/4)) print(np.percentile(sigma,95)) print(np.percentile(sigma,5)) print(np.sqrt((((x-x.mean())**2)/4).sum()))[/FONT]
I kept on telling him that. And he kept on calling me a bully. At least something is sinking in.LOL. Guess he figured out using his real name wasn't the wisest.
Bryans' behavior here, when compared to his Youtube channel videos, is bazar. Is this cat posting here really Bryan? Is this confirmed?
I take a bit more practical view, although I 100% agree that herd mentality infects Data Science just as bad as everyone else (Oh let me guess, another student wants to do their project on Large Language Models. Yes, you with your hand up you are going to ask why I didn't use a transformer)Bayes overfits data and have limited application of usefulness (I’m not saying Bayes is useless. I’m saying Bayes isn’t what they sold it to be). In fact, a tech company that hired a team Bayesian Statisticians fired all of them because their models were garbage.
The priors are picked with hardly any evidence to support their value. Then the priors are updated to fit the data through Frequentist approaches. Then the model overfits the data.
There has been big brain research statisticians argue how useless Bayes is and reality has mirrored it. The entire Data Science community moves like a flock of birds to the next best thing and Bayes has never been the next best thing.
Bayes is a tool. A great tool to have in your toolbox. But having the world's best hammer, doesn't mean every project becomes a nail. All models are wrong, some are however, useful.
And having been part of the "We're starting a data science team" in several companies most companies don't know shit about data or how to use it or data scientists and end up wasting money with a "Data Driven Approach" or "AI assisted Tools" so it may not have even been the result of Crappy Bayesian. My director kept telling me how he wanted the results and how he could get them and why couldn't I produce those results and I kept telling him: You can't just ignore random points because they disagree with your thoughts. "We need 70% accuracy on our model"
Ok so top choice: "Would you like to change your password" as default. 85% accuracy. I'm gonna go surf the web rest of the day while you assign your AI guy some rando business shit.
Ugh. Nam flashbacks.
As to the random number stuff, it got covered. There are no theories that rely on randomness and what we call randomness is often properly termed chaos (think butterfly effect) in which the initial conditions of the problem play an important role in the outcome. But as far as things like photons spontaneously emitting a electron-positron pair at random, we can account for that with every increasing precision.
I take a bit more practical view, although I 100% agree that herd mentality infects Data Science just as bad as everyone else (Oh let me guess, another student wants to do their project on Large Language Models. Yes, you with your hand up you are going to ask why I didn't use a transformer)
Bayes is a tool. A great tool to have in your toolbox. But having the world's best hammer, doesn't mean every project becomes a nail. All models are wrong, some are however, useful.
And having been part of the "We're starting a data science team" in several companies most companies don't know shit about data or how to use it or data scientists and end up wasting money with a "Data Driven Approach" or "AI assisted Tools" so it may not have even been the result of Crappy Bayesian. My director kept telling me how he wanted the results and how he could get them and why couldn't I produce those results and I kept telling him: You can't just ignore random points because they disagree with your thoughts. "We need 70% accuracy on our model"
Ok so top choice: "Would you like to change your password" as default. 85% accuracy. I'm gonna go surf the web rest of the day while you assign your AI guy some rando business shit.
Ugh. Nam flashbacks.
As to the random number stuff, it got covered. There are no theories that rely on randomness and what we call randomness is often properly termed chaos (think butterfly effect) in which the initial conditions of the problem play an important role in the outcome. But as far as things like photons spontaneously emitting an electron-positron pair at random, we can account for that with every increasing precision.
I typically won’t debate anyone on here as I of all people have built thousands of models just to have my assumptions disproven by the data. Bayes just isn’t as good as it was sold to be and I’ll leave it at that.
I got out of data science because people were calling theirselves “Data Scientists” because they knew how to:
import sklearn.abc as abc
Or because they knew how to use and access analytical databases.
Then they get on LinkedIn and talk about overcoming impostor syndrome.
No, it’s because they aren’t what they sold themselves to be and they know it. The entire community is full of frauds.
I had graduate classes with “Data Scientists” who admitted they did not know mathematics or statistics well. They should have never been given the title. An entire community built on APIs, copy and pasting scripts, and using LLMs to produce their code. It’s embarrassing.
Bryans' behavior here, when compared to his Youtube channel videos, is bazar. Is this cat posting here really Bryan? Is this confirmed?
Controlled environment. Turns off comments on his videos. Kinda like that "everyone has a plan until they are punched in the face."
If you're used to being the smartest person in the room, or in a position where people never tell you that you're wrong......it's a fair chance you might not handle it well when it happens.
Roger that.Controlled environment. Turns off comments on his videos. Kinda like that "everyone has a plan until they are punched in the face."
If you're used to being the smartest person in the room, or in a position where people never tell you that you're wrong......it's a fair chance you might not handle it well when it happens.
What would you know, you &$@@&#%}{}*+€! bully!!!If you're used to being the smartest person in the room, or in a position where people never tell you that you're wrong......it's a fair chance you might not handle it well when it happens.
lol the above is a simulation of various deleted Bryan Z threads
Last edited:
Like athletes who call themselves “warriors.”Controlled environment. Turns off comments on his videos. Kinda like that "everyone has a plan until they are punched in the face."
Nope.
-Stan
Can we make sure this thread doesn't get deleted? I read the other threads and there was some good explanations /knowledge drops from @Rio Precision Gunworks and @JB.IC and a few others. That knowledge should be retained. If it was possible to recover the good parts of the deleted threads and merge them together that should be kept around.
Last edited:
