I was recently trying to compare the accuracy of some loads. I shot a few 5-shot groups and saw small differences in the group size, but the question was whether these differences were real or were just statistical fluctuations? How many shots must be compared before one can distinguish two loads? I didn’t find any guidance on the Web, so I did a simulation which I want to share this with the group. Some of the results surprised me, and pointed out errors in my thinking about the accuracy of my rifle and my shooting.
I. WHY DO THIS?
Ballistics measurements are governed by statistics. Quantities such as muzzle velocity or point of impact vary randomly, and these fluctuations can be described using statistical methods. Often determining these random fluctuations is more important than the actual values. For example in ammo development we chronograph the velocity of a load, but we care as much or more about the fluctuations (standard deviation) of the measured velocities for a string of shots. It is a small standard deviation (SD) which produces accuracy and the absolute velocity is of secondary importance.
The question which comes up is how to compare measurements of fluctuations? Measurements of group size will fluctuate due to statistical variations. How does one calculate the expected standard deviation of a measured standard deviation? For example: Load A produces a 5-shot group with Extreme Spread (ES) of ½-inch, and Load B produces a 5-shot group of 1”. Is Load A necessarily more accurate than Load B, or is the difference just due to chance? How many 5-shot groups must be fired to definitively distinguish the accuracy of two loads? I found little guidance about these questions in standard references on statistics. Statistics books all discuss using the standard deviation (SD) to characterize uncertainties in the mean value, but nobody discusses the “standard deviation of a measured standard deviation”.
We can learn a lot from shooting experience but it takes a lot of ammo, and a lot of care and patience, to study these fluctuations systematically. So I decided to build a simple computer model which would allow me to answer the question of how to conduct a ladder test of a set of loads with sufficient precision to distinguish the innate accuracy of the loads. These simulations correspond to shooting 10,000 rounds of ammunition under constant conditions, something impossible to do with real ammo.
II. THE MODEL
The model was done using the Microsoft Excel spreadsheet program. Hits are thrown with horizontal (x) and vertical positions chosen randomly according to Normal distributions (bell curve) with mean position = 0 units, and Sigma = 1.0 unit. The unit depends upon the particular rifle/ammo combinations; it could be ¼-MOA or 1-MOA. It does not matter for the discussion. We can then look at how the shape of the hit patterns, and quantities such as the Extreme Spread (ES) or vertical dispersion (ESY), vary due to random fluctuations
positions chosen randomly according to Normal distributions (bell curve) with mean position = 0 units, and Sigma = 1.0 unit. The unit depends upon the particular rifle/ammo combinations; it could be ¼-MOA or 1-MOA. It does not matter for the discussion. We can then look at how the shape of the hit patterns, and quantities such as the Extreme Spread (ES) or vertical dispersion (ESY), vary due to random fluctuations
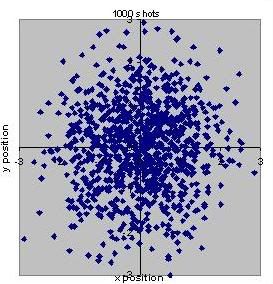
The distribution of the 1000 shots is shown below. The average group size is 1 unit horizontal by 1 unit vertical.
III. QUALITATIVE RESULTS
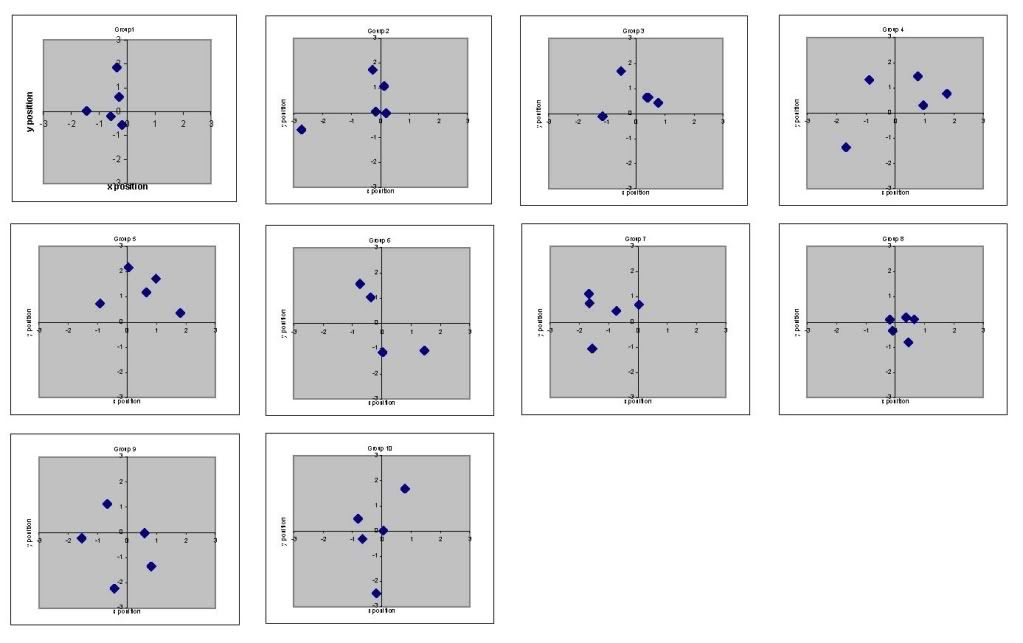
Below are 10 representative 5-shot “targets”, graphs of the x-y hit positions. (Sorry about the small print.) The groups are numbered 1-10; 1-4 in the first row, 5-8 in the second row, and 9-10 in the bottom row. The scales go from -3 units to +3 units horizontal and vertical with tick marks at 1 unit intervals. Do these targets look familiar?
Lets look at a few groups.
Group 3 and 8 – nice and tight; two shots overlaps in group 3
Comment – “My rifle is very accurate if the shooter does his part”.
Groups 2 and 4 – group plus flier
Comment – “I had a nice group going except for that pesky flier. Must be a problem with my shooting technique."
Groups 6 and 10 – vertical stringing
Comment - “This load must not be a velocity node.”
Group 1 and 7 – off to the left
Comment – “sights must be off.”
Group 5 – high
Comment – “Damn it happened again! My scope must be loose.”
Group 4 and 9 – large and diffuse
Comment – “Maybe I should clean the barrel.”
Of course, these comments are all wrong! All of these groups are produced by the same random distributions, and the variations in the size and shape of the groups occur purely by chance. In a sample of ten 5-shot groups, some will be really small, others will have a flier, miss the point of aim, or just be maddeningly big. That really nice group is only about half the average size, and it greatly overstates the intrinsic accuracy of the rifle.
If we fire just one 5-shot group of each ammo, and Load A happened to produce a group like #8 and Load B happened to produce one like #9 or #10, we could erroneously conclude that ammo B is worse than ammo A, even though they actually are identical. So what to do?
IV. QUANTITATIVE RESULTS
There are many methods proposed to quantify the size of a group. I chose to focus on two: the Extreme Vertical Spread (ESY) and the Extreme Spread (ES). I pick these because they are relatively easy to measure, and my results indicate they are about as good as other more time-consuming methods. (More about this at the end.)
ESY is the height of the group. We expect it to depend mainly on the consistency of the ammo, whereas the Horizontal Spread is more influenced by additional factors such as cross wind or canting the rifle. However if wind and canting are under control, the horizontal and vertical distributions should be very similar for a good rifle.
ES is the distance between the two most separated hits in the group
I chose to “fire” 5-shot groups because this is the size of my magazine. One might as well fire on a different target after a reload, since the results can always be combined later. 3-shot groups show larger fluctuations than 5-shot groups; but if the same total number of shots are compared, the precision should be the same.
To more accurately quantify the fluctuations in ESY and ES, I “fired” 2000 5-shot groups (10,000 rounds total) and obtained the following results:
Average ESY = 2.28
SD of ESY = 38% x ESY
Average ES = 3.03
SD of ES = 27% x ES
where SD is the standard deviation of the size distribution expressed as a percentage (that is the fractional variation in the ESY or ES values). The percentages are independent of the units, so these conclusions apply equally well to a rifle shooting ½-MOA groups as to one shooting 2-MOA groups.
The simulations show that for a typical set of ten groups (such as the 10 groups pictured above) the ESY of the individual groups varies from about 45% to 170% of the average group height. So the size variation among ten randomly selected groups will be nearly a factor of 4. Said differently, we can expect that out of a set of 10 groups, some groups will be only about half the average height and others will be nearly double the average. Just as we see in the pictures above.
The variations are smaller if one uses ES to characterize the group size. ES is a better way to measure group size if we believe that wind gusts and rifle cant are under control (horizontal and vertical sizes are similar on average). This makes sense since ES uses both vertical and horizontal information, and the statistical fluctuations should be somewhat averaged out when these are combined. ES typically varies from 60% to 150% of the average size – variation of about 2.5-times among a sample of ten groups. However, these variations are still too large. Thus, it is not very useful to only shoot one 5-shot group at each step of a load ladder and expect this will adequately characterize a load.
One can improve the accuracy by averaging the sizes of a few groups. I looked at the effect of taking a 5-group average (of 5 shots groups, 25 rounds total) and 10-group average (50 rounds) at each step of the ladder. Numerically the simulation finds that the average ES of five groups has a fractional standard deviation of 12%, and the average of ten groups has a fractional SD of 8%.
The conclusion is that the 5-group average can distinguish loads which are about 24% different, and the 10-group average can distinguish loads which are 16% different. Where “distinguish” means at the level of two standard deviations or 90% confidence limit. Said another way, if Load B produces a 10-group average size which is 16% larger than that of Load A, then there is a 90% chance that the statement “Load B is worse than Load A” is true. Better certainty requires firing and impractical number of groups. One can never be 100% certain.
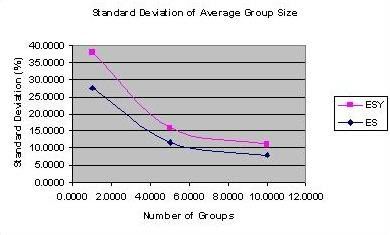
The plot below shows how the error on the average group size depends upon the number of groups included in the average. The lines are just to guide the eye – they do not represent any theory. Both the Extreme Spread and Vertical Spread are shown; again ES is the better measure all else being equal. The improvement in precision is rapid at first and becomes less rapid as more groups are included in the average.
Many other, more complicated, methods have been proposed to quantify group sizes. One method I looked at is the average radius of the group. This is touted to be better than ES because it uses all 5 of the hits, not just the two extreme hits. Including more information should improve the statistical precision of the determination. However, this method has the disadvantage that one must know the average point of impact, which will vary with the load velocity and is only determined after firing many groups and much tedious analysis. So this method is not very practical in my opinion. Also the SD of the average radius is not much better than for the ES. My simulation gives an SD of 22% for average radius of a group as compared to 27% for the ES. I don’t think this small improvement is worth the time and effort.
The reason that average radius is not a lot better than ES is that ES does actually use information from all 5 hits, not just two. The additional information is that the separations of all the pairs in the group are less than the separation of the extreme shots. This can be written mathematically as a set of inequality bounds on the pair separations of all hits; so the ES measurement includes more than two degrees of freedom.
V. CONCLUSIONS
• Extreme Spread is a better measure of ammo quality than is Vertical Spread, assuming that the wind and rifle cant are not factors. This is because ES includes both horizontal and vertical information. Measures such as average radius or standard deviation of a group distribution are somewhat better than ES, but much more difficult to calculate. It would be easier just to use ES and average more groups to improve the precision.
• For individual groups, variations of 2x or more in Extreme Spread are to be expected even for a small sample (such as 10) of groups. The very good groups overstate the rifle’s intrinsic accuracy. Fliers, horizontal or vertical stringing, groups missing the POA, and overly large groups are typical statistical variations in group morphology. These are not necessarily caused by shooting errors.
• Shooting a ladder with only one 5-shot group at each step will probably not be useful and could lead to erroneous conclusions. Many arguments over which load or reloading technique is best probably stem from not taking enough data.
• The average size (ES) of 4 or 5 groups is much more precise than using just a single 5-shot group. The average of 10 groups is even better, but the improvement in precision slow beyond that point. There will be practical limits to how precisely a load can be characterized.
• I suggest that a good strategy is to first shoot a ladder with 25 rounds of each load; five 5-shot groups. If this does not distinguish the loads, or find the accuracy nodes, then repeat the ladder and combine the results. If there is still no difference then pick a load and start shooting.
I. WHY DO THIS?
Ballistics measurements are governed by statistics. Quantities such as muzzle velocity or point of impact vary randomly, and these fluctuations can be described using statistical methods. Often determining these random fluctuations is more important than the actual values. For example in ammo development we chronograph the velocity of a load, but we care as much or more about the fluctuations (standard deviation) of the measured velocities for a string of shots. It is a small standard deviation (SD) which produces accuracy and the absolute velocity is of secondary importance.
The question which comes up is how to compare measurements of fluctuations? Measurements of group size will fluctuate due to statistical variations. How does one calculate the expected standard deviation of a measured standard deviation? For example: Load A produces a 5-shot group with Extreme Spread (ES) of ½-inch, and Load B produces a 5-shot group of 1”. Is Load A necessarily more accurate than Load B, or is the difference just due to chance? How many 5-shot groups must be fired to definitively distinguish the accuracy of two loads? I found little guidance about these questions in standard references on statistics. Statistics books all discuss using the standard deviation (SD) to characterize uncertainties in the mean value, but nobody discusses the “standard deviation of a measured standard deviation”.
We can learn a lot from shooting experience but it takes a lot of ammo, and a lot of care and patience, to study these fluctuations systematically. So I decided to build a simple computer model which would allow me to answer the question of how to conduct a ladder test of a set of loads with sufficient precision to distinguish the innate accuracy of the loads. These simulations correspond to shooting 10,000 rounds of ammunition under constant conditions, something impossible to do with real ammo.
II. THE MODEL
The model was done using the Microsoft Excel spreadsheet program. Hits are thrown with horizontal (x) and vertical
The distribution of the 1000 shots is shown below. The average group size is 1 unit horizontal by 1 unit vertical.

III. QUALITATIVE RESULTS
Below are 10 representative 5-shot “targets”, graphs of the x-y hit positions. (Sorry about the small print.) The groups are numbered 1-10; 1-4 in the first row, 5-8 in the second row, and 9-10 in the bottom row. The scales go from -3 units to +3 units horizontal and vertical with tick marks at 1 unit intervals. Do these targets look familiar?

Lets look at a few groups.
Group 3 and 8 – nice and tight; two shots overlaps in group 3
Comment – “My rifle is very accurate if the shooter does his part”.
Groups 2 and 4 – group plus flier
Comment – “I had a nice group going except for that pesky flier. Must be a problem with my shooting technique."
Groups 6 and 10 – vertical stringing
Comment - “This load must not be a velocity node.”
Group 1 and 7 – off to the left
Comment – “sights must be off.”
Group 5 – high
Comment – “Damn it happened again! My scope must be loose.”
Group 4 and 9 – large and diffuse
Comment – “Maybe I should clean the barrel.”
Of course, these comments are all wrong! All of these groups are produced by the same random distributions, and the variations in the size and shape of the groups occur purely by chance. In a sample of ten 5-shot groups, some will be really small, others will have a flier, miss the point of aim, or just be maddeningly big. That really nice group is only about half the average size, and it greatly overstates the intrinsic accuracy of the rifle.
If we fire just one 5-shot group of each ammo, and Load A happened to produce a group like #8 and Load B happened to produce one like #9 or #10, we could erroneously conclude that ammo B is worse than ammo A, even though they actually are identical. So what to do?
IV. QUANTITATIVE RESULTS
There are many methods proposed to quantify the size of a group. I chose to focus on two: the Extreme Vertical Spread (ESY) and the Extreme Spread (ES). I pick these because they are relatively easy to measure, and my results indicate they are about as good as other more time-consuming methods. (More about this at the end.)
ESY is the height of the group. We expect it to depend mainly on the consistency of the ammo, whereas the Horizontal Spread is more influenced by additional factors such as cross wind or canting the rifle. However if wind and canting are under control, the horizontal and vertical distributions should be very similar for a good rifle.
ES is the distance between the two most separated hits in the group
I chose to “fire” 5-shot groups because this is the size of my magazine. One might as well fire on a different target after a reload, since the results can always be combined later. 3-shot groups show larger fluctuations than 5-shot groups; but if the same total number of shots are compared, the precision should be the same.
To more accurately quantify the fluctuations in ESY and ES, I “fired” 2000 5-shot groups (10,000 rounds total) and obtained the following results:
Average ESY = 2.28
SD of ESY = 38% x ESY
Average ES = 3.03
SD of ES = 27% x ES
where SD is the standard deviation of the size distribution expressed as a percentage (that is the fractional variation in the ESY or ES values). The percentages are independent of the units, so these conclusions apply equally well to a rifle shooting ½-MOA groups as to one shooting 2-MOA groups.
The simulations show that for a typical set of ten groups (such as the 10 groups pictured above) the ESY of the individual groups varies from about 45% to 170% of the average group height. So the size variation among ten randomly selected groups will be nearly a factor of 4. Said differently, we can expect that out of a set of 10 groups, some groups will be only about half the average height and others will be nearly double the average. Just as we see in the pictures above.
The variations are smaller if one uses ES to characterize the group size. ES is a better way to measure group size if we believe that wind gusts and rifle cant are under control (horizontal and vertical sizes are similar on average). This makes sense since ES uses both vertical and horizontal information, and the statistical fluctuations should be somewhat averaged out when these are combined. ES typically varies from 60% to 150% of the average size – variation of about 2.5-times among a sample of ten groups. However, these variations are still too large. Thus, it is not very useful to only shoot one 5-shot group at each step of a load ladder and expect this will adequately characterize a load.
One can improve the accuracy by averaging the sizes of a few groups. I looked at the effect of taking a 5-group average (of 5 shots groups, 25 rounds total) and 10-group average (50 rounds) at each step of the ladder. Numerically the simulation finds that the average ES of five groups has a fractional standard deviation of 12%, and the average of ten groups has a fractional SD of 8%.
The conclusion is that the 5-group average can distinguish loads which are about 24% different, and the 10-group average can distinguish loads which are 16% different. Where “distinguish” means at the level of two standard deviations or 90% confidence limit. Said another way, if Load B produces a 10-group average size which is 16% larger than that of Load A, then there is a 90% chance that the statement “Load B is worse than Load A” is true. Better certainty requires firing and impractical number of groups. One can never be 100% certain.
The plot below shows how the error on the average group size depends upon the number of groups included in the average. The lines are just to guide the eye – they do not represent any theory. Both the Extreme Spread and Vertical Spread are shown; again ES is the better measure all else being equal. The improvement in precision is rapid at first and becomes less rapid as more groups are included in the average.

Many other, more complicated, methods have been proposed to quantify group sizes. One method I looked at is the average radius of the group. This is touted to be better than ES because it uses all 5 of the hits, not just the two extreme hits. Including more information should improve the statistical precision of the determination. However, this method has the disadvantage that one must know the average point of impact, which will vary with the load velocity and is only determined after firing many groups and much tedious analysis. So this method is not very practical in my opinion. Also the SD of the average radius is not much better than for the ES. My simulation gives an SD of 22% for average radius of a group as compared to 27% for the ES. I don’t think this small improvement is worth the time and effort.
The reason that average radius is not a lot better than ES is that ES does actually use information from all 5 hits, not just two. The additional information is that the separations of all the pairs in the group are less than the separation of the extreme shots. This can be written mathematically as a set of inequality bounds on the pair separations of all hits; so the ES measurement includes more than two degrees of freedom.
V. CONCLUSIONS
• Extreme Spread is a better measure of ammo quality than is Vertical Spread, assuming that the wind and rifle cant are not factors. This is because ES includes both horizontal and vertical information. Measures such as average radius or standard deviation of a group distribution are somewhat better than ES, but much more difficult to calculate. It would be easier just to use ES and average more groups to improve the precision.
• For individual groups, variations of 2x or more in Extreme Spread are to be expected even for a small sample (such as 10) of groups. The very good groups overstate the rifle’s intrinsic accuracy. Fliers, horizontal or vertical stringing, groups missing the POA, and overly large groups are typical statistical variations in group morphology. These are not necessarily caused by shooting errors.
• Shooting a ladder with only one 5-shot group at each step will probably not be useful and could lead to erroneous conclusions. Many arguments over which load or reloading technique is best probably stem from not taking enough data.
• The average size (ES) of 4 or 5 groups is much more precise than using just a single 5-shot group. The average of 10 groups is even better, but the improvement in precision slow beyond that point. There will be practical limits to how precisely a load can be characterized.
• I suggest that a good strategy is to first shoot a ladder with 25 rounds of each load; five 5-shot groups. If this does not distinguish the loads, or find the accuracy nodes, then repeat the ladder and combine the results. If there is still no difference then pick a load and start shooting.




