-
Having trouble using the site?
Contact support
Avoid this pitfall with distance/target based ladder test
- Thread starter Feniks Technologies
- Start date
thanks
ive read that before as well
that information would confirm positive compensation for a rimfire etc
but it doesnt speak about (as it wasnt in his hypothesis so i didnt expect it) about tuning for different linear "groups" along the lines of what im looking for
he did say that groups are more round in shape because of bullet irregularities etc, so that would change my perfect line to a very flat oval
unless someone explained or i missed it, tuning a barrel for compensation is only applicable on the vertical axis then something else is going on because the barrel moves in more directions than the vertical
which would mean "shrinking" of vertical is because of or in-spite of positive compensation
laymens terms...if we cant change the angle of the group by manipulating the same variables as tuning for positive compensation then we cant say with certainty what we are doing is the exact reason for the outcome
in my day job:
we test the vitamin on the way in
we put the vitamin in the blend
we run the product at correct spec
the FDA still requires a QC test for potency before shipping
without the final test, the product may still pass potency
but there is not validation that its "guaranteed by input"
brian
Not being one of the long time experts here, I nonetheless have wondered at discussions about barrel harmonics that seem to treat the subject as if the vibration was only in the vertical axis....something for which I do not see any rational justification.
To be fair, most everyone readily admits there isn’t just a vertical motion. Then some get further into the weeds about tuning horizontal.
Also to be fair, this thread was *never* about positive compensation being valid or invalid. It’s just where 3 or 4 people decided to take the conversation for whatever reason.
It was simply brought about due to another poster having ladder test issues in another thread where the data he provided was showing what he thought was a “node” when it was just simply some noise brought on by charge weights impacting at the high and low side.
Every week we help people with ammo issues via phone calls and texts. This is one of the common issues we see. Noise being interpreted for something else. This was just a post on a common issue we run into.
That’s it, nothing more, nothing less. Others decided to turn it into a debate on positive compensation.
Two final points since you seemed determined to go down this road:
1: you’ve completely gone off topic
2: while I’m not saying positive compensation isn’t a thing….
You cannot back up any of the claims in this post with any repeated testing. Countless people have ran their positively compensated barrels over doppler radar monitoring the velocity, BC, and entire flight of the projectile.
Thus far, none have show waterlines that don’t match up with that data. Sure, some exhibit some that would appear to be head scratchers for a brief time, only to not exhibit it long term and repeatable.
Believing in statistics doesn’t mean you believe or disbelieve anything. It just means that you understand that small sample size testing is next to worthless to prove or disprove anything.
If someone could show me a statistically significant test that show a tiny magical elephant flew out the muzzle of the barrel and helped the bullet on its way…….well, I’d be trying to figure out what flavor peanuts make him happy.
Very interesting read but I'm struggling to see the practical application.
Feniks, how do you land on any given powder charge? I've just grabbed a magnetospeed and am trying to revamp my current load development.
I understand that there are miss interpretations with small sample size but are you shooting an OCW with 30 rounds each? Like I said. I'm missing the practical application of this.
Feniks, how do you land on any given powder charge? I've just grabbed a magnetospeed and am trying to revamp my current load development.
I understand that there are miss interpretations with small sample size but are you shooting an OCW with 30 rounds each? Like I said. I'm missing the practical application of this.
The groups themselves render your I’ll-conceived speculation moot. Replicate it and find out
The practical application is for those doing POI ladder tests at distance.
This method is about as popular as OCW (which is done @ 100yds).
Ladders like this are typically done at 600 and 1k yds.
As far as practical application for not shooting 30 rounds, the implication there is that for most shooters, you’re better off loading to a speed and then loading consistent ammo than you are pawing around randomly in an OCW that is mostly noise.
It’s actually the opposite.
If shooter A shoots a .2moa group @ 1k yds…..
If you aren’t monitoring the speeds, you can’t say if something is or isn’t. It’s impossible to say it’s because of positive compensation, as well as it’s impossible to say it’s because the ES of the velocity was tight.
Also, everyone always says “well, look at all the groups that have a chrono and are smaller than the chrono says.”
The problem with that logic is that you only looked at the “good” groups. What happens when the same shooter shoots a group that’s larger than the velocity spread and/or his positively tuned barrel? No one every records or looks at that. It’s written off as a bad trigger press or lighting, or wind or whatever.
For you to use the “good” examples, you need to collect data on the “bad.” As it’s entirely possible someone hit an X with a poorly executed trigger press and on the the cited reasons above saved him.
So, let’s say you took 10 targets from shooter A @ 1k that had the velocity tracked for every shot. And those 10 targets have a tighter water line than the velocity shows. And those targets were shot over a 3 month period.
That sounds awesome right?
Well, unless those were the only 10 targets shot, then your data is flawed and worthless. If Shooter A shot 30 and you only used 10 for the “proof” but didn’t show another 10 that show a group size larger than the velocity spread, and another 10 that were almost exactly the same…..you have to factor those in your data.
I don’t know about most of you, but I almost *never* see someone show the “bad” groups as part of their “proof.” And bad groups are required for proof.
Barrel break in is a perfect example. If 100 people use 100 different ways to break in a barrel, and none of them ruin it…..guess what? There aren’t 100 different ways to do it. There’s zero ways that work as it doesn’t matter. You barrel performed well despite your break in, not because of it.
Load development is no different. If you don’t go back and re-test the “bad” then you have zero idea if the “good” is actually anything.
there are some discussions about this horizontal harmonics. with top FClass shooters. and horizontal vibrations exists, and that's why everybody are for nice round groups, not just good vertical (at 1000m).
laurie holland mentioned that he had once barrel, which has 'perfect' vertical at long range, but unusable horrible horizontal stringing...
I show bad groups all the time Lol.
One more question. Are you also saying that both positive compensation and SD/ES should not be factors when choosing a charge weight due to small sample size and statistical errors?
If so, are the only ways to achieve better ES/SDs is to control powder charge with an fx120i (or other quality balance) and to control neck tension?
So, I'm trying to understand the confirmation tests (shooting over your Oehler, as you say) that you're doing. You keep saying that the bullets are landing where there should, fo velocity and BC, but are you also measuring their initial vector? How else can you say they are hitting where they should?
Second, if the compensation (which I don't necessarily believe in) is happening, then the things you're saying could happen due to shifts in barrel trajectory, and the fact that they land "where they should" isn't the right test. Especially if they fall in a range that is tighter than they should.
Or are you saying that you're shooting at such a large distance that the cone of impacts are totally separate for those velocities, and they never land outside their respective zones? Because if that is the case, how does one explain someone who shoots a bunch of 10s at 1k with large ES?
Also, just to clear up a couple of things: small sample size isn't the deal breaker. There's nothing magical about a sample size of 30. That's just the point where the t-distribution becomes a close approximation of the normal distribution. It never really gets there until infinity, but 30 is a rule of thumb... It's not magic. The critical values for a 99% confidence interval on a sample of 20 is about as far from 30 as 30 is from infinity. 30 is by no means a "minimum" requirement, it's just a conventional one. More is always better. The usual rule with small samples is more to use then to weed out "bad" things than to confirm good, as your ES and group sizes can't shrink.
Does a barrel really have an effect on ES/SD or is that just a testament to precision reloading?
Can you have low ES/SD in bad shooting barrel?
If the longer the barrel the more harmonics and barrel whip come into play. And finding a node more important. At what length is harmonics and whip not a factor and finding a node a moot practice? If that's the case there's probably a sliding scale.
Can you have low ES/SD in bad shooting barrel?
If the longer the barrel the more harmonics and barrel whip come into play. And finding a node more important. At what length is harmonics and whip not a factor and finding a node a moot practice? If that's the case there's probably a sliding scale.
velocity of bullet consists of everything that efects on bullet. so bullet shape, weight, jacket, barrel, primer, powder, volume of brass, neck tension, thickness of brass that expand... everything that is not theoreticaly the same as before. even freebore is changing. only chamber we can assume that stays the same.
in theory imho...
Currently, there isn’t anything that can measure (at least that anyone doing any testing most of us would have access to) the initial vector.
However, different types of testing fixtures have been used that hold an entire rifle, a barreled action like a chassis would, and others that clamp around the muzzle. No tests that I’m aware of have produced any meaningful data which suggests bullets are consistently impacting along a waterline which doesn’t line up with velocity + BC math.
And of course more is always better. 30 rounds is just where the confidence level is enough there’s much more signal than noise. As in rounds after 30 have a significant diminishing return on your data.
As to the explanation about shooting 10’s with a large ES.
Most matches don’t allow velocity to be monitored. So that hampers data significantly. If chronos were run at matches, we’d have tons of data.
The problem with the “10’s being shot with bad ES” is it’s almost always the good groups being shown off.
To make that data valid, those same shooters would need to record/release data on the groups that didn’t shoot tighter than the ES would allow.
For example, if 50% of your 10 ring groups were better than the ES and 50% of your groups did worse what the ES says and you dropped into the 9 ring……that’s a far different picture than 90% and 10%.
So, until the data for all is recorded/shared, the data released by people saying “I just shot a 3” group @ 1k but the ES said it should have been 12”” is all but worthless as anything other than bragging rights. It neither proves nor disproves anything at all.
Then when people show up to somewhere like Applied Ballistics to show them their compensated barrel and loads…….they are now required to have every single shot recorded over multiple days. Magically, the signal they claimed they had ends up being noise…..and the long term data evens out.
I believe someone mentioned it above. You can *generally* weed out “bad” loads with small sample sizes. As when it starts out bad enough that the data won’t reign itself in for the long haul, no need to continue.
And yes, as far as SD and such, if you’re using the correct burn rate for the capacity and bullet weight, brass prep and powder drop will have the biggest influence on your velocity numbers.
However, *most* shooter’s loads are much closer in quality than the initial testing shows.
We perform a test relatively often with shooters who would like to see this theory play out live:
- shooter does their load development however they like. They decide what their best and worst is.
- shooter brings those recipes to us. We help them load it to make sure it’s consistent
- we label the boxes, but the shooter is not allowed to know which round they are shooting
- we decide which round they shoot each time and record the data. Be it velocity, group size at variance distances, etc.
- we shoot enough rounds (typically 30 for each test) to be very confident in the results.
Chrono data usually ends up being extremely close.
Group size is also extremely close as we use the same seating depth and generally speaking that usually performs independent of powder charge weights.
That’s not to say the better load doesn’t still beat out the worse load (sometimes the worse load actually performs better), but it’s always much, much closer than the shooter expected or their low round count test showed initially. And if the discipline they are shooting is practical/steel, the difference is almost always not enough to justify the amount of time spent on the testing.
For practical/steel shooting, it’s rare to see a “bad” shooting barrel. Some are “hammers” and others are average.
In disciplines like BR and F, there are absolutely barrels that perform better. That’s a whole other topic. But I don’t think anyone believes they know why or can predict it. It’s a matter of testing and deciding if a barrel meets their standards. Again, whole other topic.
I’ve had barrels with fire cracking so bad it won’t shoot well, but velocity wasn’t bad. So it’s definitely possible.
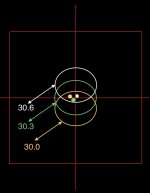
Assuming a load can hold waterline every shot is ridiculous, the pics we see of great ones are no different than the wallet groups fudds carry around, BFD
Let's start here with this pic, as I believe in OCW tests, and Long's OBT, now I have no way of measuring OBT, but like I mentioned earlier, one shot ladder tests are a waste of resources. In this pic, a simple OCW test with 5 rds would eliminate the top charge, which now narrows the charge range from 29.9-30.4, If an OCW test was done in .1gr increments, most likely a satisfactory charge will be found, and .1gr variance in the powder charge either side will not upset too much.
You refer to cone of accuracy, ok
Let's say my reasonable cone of accuracy over a set period of time is 10" at 1000 yards.
So if we did everything the same, cleaning, rd counts, etc...., and skill level is as close to equal as can be
And your cone of accuracy is also 10" at 1000 yards using your methods.
Under ideal conditions, same-same, side by side we each shoot 3- 10 shot groups.
If we both went 8/10 on all 3 samples, I know what you will call my lack of reaching a perfect goal, but how will you explain yours?
I have shot OCW tests at 500 yards minimum with rifles for over 7 yrs. First, I cherry pick my charge ranges based off chrono numbers too.
In all my time in doing this, shooting right tw barrels, as I go up in charge weights, I have Never seen a higher charge weight exhibit a straight vertical rise, ever. If I have 2 charges, hopefully 3 that retain close to the same impact as related to the POA, by the time my charges will not fall in this parameter, they impact right, some may be above, but more times than not, it is now low right, and by moving, does not mean I am immediately into another node as I hate to call it. But typically, for me using M24 contour barrels, it will almost follow a clock pattern.
These are my facts.
So when I read a rd coming out of a barrel faster automatically goes high I find that hard to believe, not saying it will not happen. if it was against the law to shoot over 600, this discussion would be moot.
Also, a prs match with a labradar on each stage would be fun to watch, of course it is not amusing when it happens to us personally, but watching a shooter chase an anomaly is fun.
Last edited:
Ok, I hope this doesn't come off as combative. I'm no believer in positive compensation (I think tuning should result in less muzzle movement), and you seem to actually be doing more real testing than most people. I'm just trying to understand the actual test that you're doing. Let's leave the vector aside, as I agree the vector can't be measured, and surely clamping the gun is the best we can do anyway. Although, if you're clamping the muzzle, that's an issue, as the whole positive compensation requires the muzzle to move doesn't it?
If what you're doing is saying "these bullets fall within the a predicted confidence interval (of whatever % confidence you're going with) based on velocity and BC" then I'm not sure that's actually the right test. Especially if the predicted confidence intervals of all the observed velocities overlaps, and the shots are falling into the confidence interval of all those velocities. Then, your test doesn't have the power to really say much at all. Sure, *if* you found bullets landing way outside the predicted interval, that might support positive compensation, but it's not true to say "since we don't see that, it's not there". Absence of evidence is not evidence of absence, as they say. Perhaps you're actually doing something else though.
Two ways I would look into this: first, given a load with a certain average velocity, do lower velocity shots tend to land high within their confidence interval and do higher velocity shots tend to land lower within theirs? Do the impacts tend to have lower dispersion (variance in the waterline) than predicted? Both of those outcomes would point towards a "tuning" effect, but wouldn't land outside of predicted intervals.
Second, positive compensation seems to say that the launch angle changes for shots based on velocity. Ok, you can't measure the angle, but we're clamped so the bore should be nominally pointed in the same direction as best we can control. But launch angle isn't the only prediction... along with this, there should only be one "tuned" range where shots return to a small dispersion. There should also be a point of maximum angular dispersion at an intermediate range... why not test that? If you know where the groups are supposed to be tight, you can calculate a flight path and find where the maximum dispersion is supposed to be. If the groups there have a smaller MOA than the farther "tuned" distance, then it wouldn't support positive compensation. If someone claims that their gun shoots tighter *everywhere* then that's not positive compensation anyway.
On the sidebar, again, 30 observations doesn't "fix" anything. For a given variable, higher numbers of observations shrinks the confidence interval, but that doesn't mean that 30 observations results in small confidence intervals and 10 results in large confidence intervals. 30 will just narrow it down, but how much isn't static. It might not help much if the variable being measured is random as hell. But it's entirely possible to have narrow confidence intervals with lower observation counts if the variable has a low variance. It's absolutely possible to have confidence intervals as wide as the ocean with 100 observations if there is a lot of underlying variation.
A real problem for us is that shooting is destructive testing, as you say, more can result in diminishing returns, and in fact can actually result in worse data. Like, more observations should narrow down our confidence intervals, but barrel fouling and wear may actually introduce more noise rather than less. We have to go for a parsimonious data collection. If someone has to shoot 30 rounds per test, is the 30th shot really going down the same bore at that point? Should we clean it? Should we not? If we then do another test of 30 rounds, how do we start to compensate for throat erosion? Especially for hot magnums and short barrel life rounds. Etc. There's no perfect way to do it.
All the things you mentioned in the first part have already been tested by several entities (Applied Ballistics being the most notable).
Nothing thus far has produced any repeatable results which would suggest that bullets are impact somewhere that would imply slower rounds leave at a higher initial vector then faster rounds which results in a smaller dispersion than velocity + bc predicts.
For example, shooter A claims he has tuned his rifle to exhibit the scenario in the photo you linked. Shooter A goes to a service like applied ballistics and attempts to demonstrate.
Thus far, zero have been able to demonstrate a repeatable scenario at the distance they have claimed their rifle exhibits positive compensation.
Also, nowhere has anyone stated 30 rounds fixes anything. It’s been clearly stated that is the point where the tide shifts and now, generally speaking, this is where you wont have large swings in your data. Can a swing happen? Of course. But it’s becoming fairly insignificant.
A flipped coin will land on its edge ~ 1/6000 times. But we don’t actually consider than an outcome as is not significant.
While the odds of say a 100 round string might be different than a 30 is a bit more likely than 1/6000, it’s still not enough to consider.
You’re asking for tests that have already been done.
Also, as I have stated, the tests many of us have performed have *included* clamped muzzle. Not only run with a clamped muzzle.
You’re picking the situation that suits your point and leaving out the others.
Sleds that hold the actual rifle and fixtures that hold a barreled action (screws and clamps) have been used as well.
None of the tests have show any data to support positive compensation.
The point being, the clamped muzzle and the non clamped muzzle should have shown significant differences. When they don’t, the implication is the launch angle isn’t what’s actually happened.
Also, worth nothing, (it’s anecdotal, but still), there have been places who have used an extremely high frame rate camera magnified on the muzzle as the bullet exits.
High enough frame rate to see the bullet rotate.
Thus far, there has been no visible indication the muzzle has a different launch angle until *after* the bullet leaves the muzzle. Then there is obvious movement.
Again, that’s anecdotal and the argument against us the launch angle is too small to visually observe.
High enough frame rate to see the bullet rotate.
Thus far, there has been no visible indication the muzzle has a different launch angle until *after* the bullet leaves the muzzle. Then there is obvious movement.
Again, that’s anecdotal and the argument against us the launch angle is too small to visually observe.
As well as I have absolutely *never* said anything like “because we can’t see it, it’s not there.” You have inserted that assumption.
What I have said is there has currently been zero observation of the phenomenon. That’s it. Nothing more, nothing less.
Well, obviously, we're not really getting anywhere. I'm not asking what your results have found in a summarized sense. I'm asking what tests you've done. Saying "tests have already been done" doesn't tell me how they did the tests. But that's fine. Like I said, I don't personally buy into positive compensation anyway. I'm just trying to figure out how someone tested it and how they assessed the data.
And again, perhaps we're speaking past each other, but it seems your understanding on sample size (re: n=30) and it's effect on significance is a bit off. It's not worth arguing about, however. It's probably just loose vs strict interpretations of the terminology.
One thing about the terminology positive compensation is when the rounds land inside to the calculated vertical dispersion and negative compensation lands outside to the calculated vertical. The calculated vertical assumes the same launch angle. Most every rifle will exhibit negative compensation if the velocities are different meaning they left at a different muzzle position. but if the velocities are the same meaning in bore time is the same it will shoot just as well no matter what the pattern is because they left at the same muzzle position. This providing all is well with the gun and its components.
Tim in Tx
Tim in Tx
The key here is the effecting variables. Vibrations have different drivers so variables are often inserted in testing not really knowing if they are actually effecting the result. Barrel movements are no different .But by many years of testing many types of tuning systems the non effecting variables are slowly eliminated . A barrel will move through many modes of vibrations and 90% of these modes are only after the bullet has left the barrel and only then can a barrel go to a natural frequency . The natural frequency has to be free of any damping or touching the barrel that is not solidly attached . When a bullet is in the barrel and moving the barrel physically can not vibrate in a natural state due to the bullet traveling through the barrel. However the recoil force will drive the transverse wave which is vertically oriented. This is the main effecting mode of vibrations and it has no real frequency meaning no constant during this transverse wave. the transverse wave has different patterns along this one time wave and that is what we are speeding up and slowing down with a adjustable weight.
Tim in Tx
Sounds reasonable..
Let’s follow the transverse wave idea and the 10% idea for a bit..since it seems you have a handle those possibilities.
10%
Has anyone measured and has there been any consistency in the type/amplitude of the “pre bullet leaving” barrel. I’ve clicked around for a while and never found empirical data and measurements?
If I remember the math, it takes about .002-3” to move the POI at 100 yards 1/8moa.
.003 is more than enough to measure, even with dial indicators. Have you seen any info or pics/video of that. That Info would be a game changer.
I’m thinking if a tuner or any form of vibration to accuracy manipulation (POA to POI) must be taking place in the 10% +\-. Because that’s when the barrel can be “pointed” in the wrong direction.
So logically if the 90% of vibration is after it leaves…90% of the total vibration data usually recorded is irrelevant. Unless the vibration is such that as the bullet leaves it becomes a sliding scale of sorts.
At 50% of bullet length out of the barrel X amount of “post bullet” vibration starts acting on the base of the bullet…kicking its ass so to speak.
Or
The post bullet vibration while changing the location of the actual bore once the bullet has left the barrel, allowing the pressure/gas to act on the base of the bullet erratically causing a yaw effect?
Possibly showing why 11 degree crowns are popular?
Transverse wave.
Can you send me or post information on why we know it’s a 12-6 transverse wave, or rather the reasoning for it?
Is it because the recoil lug is usually only at the 6:00 position so vibration moving in the 9:00-12:00-3:00 is path of least resistance?
I wonder if the recoil lug was a complete circle, like a donut if that would change things?
Thanks for the reply..it’s fun getting the brain moving sometimes.
I have seen a video and it did not move while the bullet was in the barrel , it needs better resolution and the position if the indicator was on a node which means no lateral movement . had the indicator been 1-2 inches back it would have moved laterally and the dial indicator would have picked it up . I have 20 years of ladder tests that show it does change in a angular fashion so one video is not proof nor is it a game changer. It would not matter how the lug is oriented because the barrel is going to bend around the heaviest side bolted to the action/ barrel assembly in most if not all cases would be the stock directly below , this is why it is vertically oriented. It is almost futile to predict amplitude or the total vertical poi change by the math mainly because there are small and many vertically oriented angular changes within the vertically oriented transverse wave . Using ladder testing I have data that shows poi changes of two inches is common and most times when I have tried to calculate the poi change using relative stiffness ratios along with offsets in weight and recoil force. The POI spread at 100yds was no where near what I had calculated. It was only through trial and error testing that I was able to do any type of measuring the total amplitudes by way of the target. I test in test conditions that eliminate wind or I just do not do the test normally. With that being said the testing was always straight up and down on every gun every time or outside with use of at least 5 wind flags in the scope view. This being with a benchrest set up where the rifle is allowed to rotate more freely in the front bag under recoil which allows for less horizontal deflection..
No doubt the muzzle blast has a effect but not like what one would think. I can cut a muzzle face , not the crown .018 out of square and it can change the POI drastically around 8-10 feet at 1000 yds but not cause any accuracy degradation that is detectable. As to the yawing effect ,with a jacketed bullet, the bullet while in the barrel it is held to a mechanical center line ,and it is subject to the curvature of the bore, during the trip down the barrel, the base pressure on the bullet hits peak pressure 4-6 inches out from the chamber at which time the bullets base compresses forward actually slightly bulging the nose of the bullet changing its shape . When the bullet exits it transitions from a mechanically held center line to a free floating center line and center of pressure based on it new shape, often referred to as CG/COP offset. This offset can actually be reduced by seating depth changes. Incorrect seating depth causes two main problems ,it makes the SD and ES grow and it causes a random dispersion. I attribute this effect of random dispersion to CG/COP offset. For that reason I have a patented suppressor design that negates this effect as well by stabilizing the bullet just as it leaves the muzzle making throat erosion non effecting variable over the life of a barrel.
Tim in Tx
Last edited:
Now we are talking...... finally, someone has something they've done with some real meat to it.... I hope you get in touch with him on this and make this happen or at least show your data. This is very interesting
positive compensation does not exists in the way that you will get smaller group at 1000y than in 500y. so everything connected with that theory is bulshit.
next real question is if our barrels have real 'nodes'; areas of smaller or no vibration (or are those areas of nodes just areas of smaller groups and no vibration is going on).
and that kind of question I sent to AB (to Litz), but they didnt answer; if they will...
I am afraid so , it does exist in a vertical respect . It is just not easy to do .Been used for years
Tim in Tx
i dont know how to do the multi post/question thing so your in yellow:
I have seen a video and it did not move while the bullet was in the barrel , it needs better resolution and the position if the indicator was on a node which means no lateral movement . had the indicator been 1-2 inches back it would have moved laterally and the dial indicator would have picked it up .
Do you know where that video is...be nice to see it..would answer a ton of questions
It would not matter how the lug is oriented because the barrel is going to bend around the heaviest side bolted to the action/ barrel assembly in most if not all cases would be the stock directly below , this is why it is vertically oriented
i guess we need to find someone with a BR rail gun that has the large barrel block. seems that might be the only way to really eliminate any outside influence other than the actual stress in the barrel material.
have you seen the same T wave with systems like a eliseo that has the action "wrapped" up in the chassis, i would think that that chassis (of if its bonded in total like some guys do) would help reduce the vertical?
one thing im not getting or im missed it in your reply;
believing bullets are consistent and not the issue, group size is math
angular movement at the shooter will create a certain group size at X distance (minus outside influences)
if a tuner/positive compensation etc have a positive or negative effect on groups as several targets that have been posted show, the group size difference i have seen is able to be measuered at the shooter.
either the:
barrel
action
stock/chassis
any combination of the three
all those added up will have to cause the muzzle of the barrel to be "off center" be a few .001's...we should be able to capture that measurement before the bullet leaves
unless the barrel is somehow acting like a jump rope with the belly flexing/amplitude more so than the muzzle?
thanks
In an extremely basic example (completely making up numbers for the example):
Two round are fired
2950
2900
For the compensation to work, at a basic level, the 2900 has to have a steeper launch angle than the 2950.
This launch angle can easily be calculated and translated into a linear number.
So, my question:
Why has no one been able to identify the different launch angle and in turn tested and verified these launch angles?
Two round are fired
2950
2900
For the compensation to work, at a basic level, the 2900 has to have a steeper launch angle than the 2950.
This launch angle can easily be calculated and translated into a linear number.
So, my question:
Why has no one been able to identify the different launch angle and in turn tested and verified these launch angles?
For those interested in the concept of Positive Compensation you might find the following work of interest.
Not wanting pour fuel to fire, but if you accept that barrels do vibrate then the theory of positive compensation is a direct extension of that action as is the use of heavy barrels.
Whether Brian has investigated this or or to what extent I do not know.
Let me pose a question for consideration. Has anyone ever developed a load and seen higher POI with lower velocity than with higher velocities?
It’s all theory and will be debated until the end of time until someone actually can repeatedly measure and show it time and time again.
As far as AB, the last I heard, no shooter had been able to bring their rifle and ammo and show different POI or smaller dispersion that what velocity and doppler accounted for.
There around be instances that show compensation, but never held up long term.
Obviously this doesn’t mean that it doesn’t exist. Just that thus far when doppler us tracking the exact BC/flight path and velocity, the bullets don’t go where the math says they shouldn’t or there isn’t an explanation other than compensation.
I believe there’s still an open invitation. So if anyone has a rifle and ammo that will consistently show the compensation, I’m sure AB would love to have you come run it over their equipment.
this is right question.
and this effect/question don't have 'positive compensation (that the groups will shrink with distance)' in it. just vibration of the barrel.
but indeed I shot the other day and saw BIG POI shift with higher velocities at 100m, but I believe that it was because some mechanical issue and heavy mirage, because POI shift was very big, 1 MOA! and groups were horrble...
Similar threads
