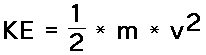Re: Buffer spring affect on accuracy???
<div class="ubbcode-block"><div class="ubbcode-header">Originally Posted By: Kombar</div><div class="ubbcode-body"><div class="ubbcode-block"><div class="ubbcode-header">Originally Posted By: RedCreek</div><div class="ubbcode-body">. So, assuming an AR was properly sprung to begin with, when that spring looses 10% of its efficiency and that loss yielded a 10% increase in carrier velocity this would in turn result in a 40% increase in energy of the carrier.
</div></div><div class="ubbcode-block"><div class="ubbcode-header">Originally Posted By: RedCreek</div><div class="ubbcode-body">Its 40%
If you increase the velocity of an object you quadruple the engery and if you double the weight you only double the energy.
Speed x weight / 64.32 = energy
I would share with you the test results from a DoD project we did, but then I would have to kill you
Show me your math...
-E </div></div>
First a list of variables used:
(F_sp = spring force, k = spring constant, s = spring displacement from equilibrium, a = acceleration, m = mass, v(s) = velocity as a function of position, v_0 = initial carrier velocity, v(s)_2 = carrier velocity when weak spring is used)
As for the part about a 10% increase in velocity:
F_sp = -k s
Once the rifle has fired and the carrier is moving rearward with velocity v_0, the acceleration of the carrier (neglecting friction) is:
a = F_sp/m = (-k s)/m
Integrate with respect to the position from spring equilibrium:
v(s)^2 = -k/m/2*s^2 + v_0^2
With a 10% loss in spring constant this becomes:
v(s)_2^2 = -.9k/m/2*s^2 + v_0^2
Divide out the 9/10, subtract the newly created remainder of v_0, substitute the identity for v(s)^2 into the v(s)_2^2 equation, move the remainder back, multiply back in the 9/10 and take the square root and you are left with:
--------------------------------------
v(s)_2 = sqrt(9/10*(v(s)^2+1/9*v_0^2))
--------------------------------------
This equation shows that the velocity of the carrier being controlled by the 10% weaker spring is dependent on the initial velocity of the carrier, and does not simply equal 10% more velocity than it would have had with a proper spring. This relationship was verified by computer model.
As for the second part of your post, kinetic energy is half the mass times velocity squared, so the original kinetic energy is m/2*v^2 (your equation would be correct for ft,lb,s units if you had remembered to square your velocity term). The kinetic energy of the carrier with the weakened spring is m/2*9/10*(v(s)^2+1/9*v_0^2). Again there is a dependency on the initial velocity, so it cannot be solved without initial conditions.
However, if the carrier velocity just so happens to be 10% greater than normal, energy would <span style="font-style: italic">still</span> not increase by 40%. The energy at 110% of an arbitrary velocity, v, is m/2*(1.10v)^2. Square that 1.10, and you are left with 1.21. At this point you can simply bring that out of the equation and you are left with the original energy calculation multiplied by 1.21. That is to say, for a 10% increase in velocity, there is a 21% increase in energy for any combination of mass and velocity.
You are getting confused with the definition of energy. Doubling, not just increasing, the velocity will quadruple the energy. </div></div>
Thank you,
I realized his error in math but just don't have the energy (or will) to respond in depth.
If you can't dazzle them with brilliance? (AKA competence in basic physics).................
Talking to Americans about matters of science and math is becoming sadly futile.
When I speak to folks from Europe I seriously seldom encounter what has become the norm here.
Even older engineers who do not stay sharp are disappointing because they will seldom believe that they are wrong and then want to analyze minutia to death.
What the hell is the matter with this country?
This shit is not that difficult if you graduated high school.
I can think of five different ways to prove the same thing, and they'll all be correct ways of looking at it (and I learned all but one way in high school).
We need to get our collective asses in gear, cause we're about to have Them handed to us.
This is not a bashing but a reality check.
We're all in the same sinking boat together.
To RedCreek
I F-up math all the time, it's what I do best.
I'm sure if this was an actual project and not a snipery post, you'd have identified the errors.
Only the steel in intimate contact with the buffer would be accelerated.
The reciprocating mass would achieve almost exactly the same velocity with no recoil spring.
A few grams of steel added to over 20 oz. of reciprocating mass will have a negligible effect for our discussion.
The carrier accelerates from zero to around 21 ft/sec (depending on recip mass) in less than 0.10"
The bullet has left the barrel after around 1 millisecond after pressure rise.
If the spring is indeed affecting accuracy, I would bet that it's an indirect cause/effect.