OK, well, shit. I'm going to jump into the ring with the Big Dogs. I hope I make it out alive. Somebody ring the bell if I stop moving, please.
I'm pretty new to long-range shooting, but I've been doing pretty hard math since before
@Lowlight went to basic, and I've been writing code since he was in Scout Sniper school. I'm formally trained in Physics. I'm very familiar with JBM's published code because I have my own version of it I use for things like replicating AB's WEZ modeling, etc.
First the thing about Physics is that if you ask a physicist how long it will take for a boulder to roll down a hill, he'll start with, "Imagine a perfectly spherical boulder on a frictionless inclined plane". If you ask him to compute wind drift, he'll say, "Imagine a spherical bullet on an infinite Euclidean plane with a wind vector that is constant". That's because once the real world gets involved, the math gets super hairy. Wind roses are trying to give you an answer that is like what you'd get from a physicist or, rather, the particular type of physicist called a ballistician.
The thing is, all the wind roses published in this thread are wrong. Terry's advice is better, but way too much work, in my opinion, because you can get the "physicist" answers with a spreadsheet where you compute angles and sines. Here is a link to the
spreadsheet I used. Of course, it's really important to know how all this shit works and be prepared for your electronics to go down. I make electronics. That's why I know they will go down. Hell, you might just forget to pack batteries. Or the stage may not allow electronics. In that case, you really need to know what the electronics are doing. That's where computing all this and writing it down becomes critical. It's also where an angle indicator or a cosine indicator (because it's cosine for the drop when shooting at an angle--not the sine), as well as a mil-dot master or equivalent become important.
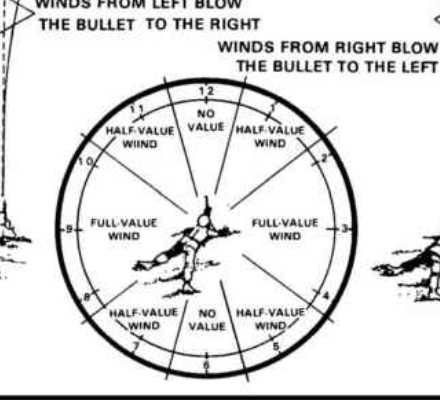
Wind drift is computed by multiplying the sine of the angle between the direction of fire and the wind angle by the full-value correction or:
sine(Wind Heading - DoF Heading) * (correction for full-value of wind speed)
It's just that simple. So, it's pretty easy to figure out the angles on a clock (each number is 30 degrees) and compute a bunch of sines. However, when you do that and you overlay it in the "half value" wind rose, you see (as
@Lowlight did) just how seriously fuck-brained it is:
Really? 4.25 o'clock? Is anyone really going to get that right in the field? Under time pressure? Also, note the following:
- "No Value" ranges from 26% left to 26% right in a very narrow angle.
- "Half Value" ranges from 26% to 79% in what is still a narrow angle.
- "Full Value" ranges from 79% to 100% to 79% in a pretty wide angle.
My conclusion is this rose works for full value winds and not much else. Remember how people talk about how a full tailwind or a full headwind are the worst? This is exactly why. Yeah, they can be switchy, but all wind is switchy. The difference is that the changes in direction at those angles have vastly greater effect on the trajectory of the bullet than they do in the "full value" range.
Which is not to mention the shooter in the middle of that rose isn't squared up behind the rifle. Poor fundamentals. Don't listen to him. (Yeah, I know back then everyone used a sling and that's the right way to shoot prone from a sling).
Now, let's look at the "3/4" rose:
Again with the half o'clocks!
- You have a swing from 11.5 o'clock to 12.5 o'clock that is 52 percentage points
- In the 60 degrees between 12.5 o'clock and 2.5 o'clock, you have a swing from 26% to 97%
- You have a narrow range of 15 degrees from 2.5 o'clock to 3.5 o'clock where you go from 97% to 100% and back to 97%
Again, good luck doing all that arithmetic in your head under time pressure!
Now, let's look at the rose that
@Lowlight made:
OK, so he isn't totally off. In fact, I'm pretty sure I've heard him say he rounded the percentages to make his rose easier to use. However, look from position 15 to position 1. There's a swing of 76 percentage points. Being a little bit off in this area is a big deal. Can you judge an angle between your DoF and the wind to better than 15 degrees? Well, that's good, but even if you get down to 5 degrees, you're still playing with a LOT of variance. You swing between 38% and 92% in 45 degrees. You better be good at this. I'm sure some of you are. Congratulations! That's why you're winning matches.
So, what's the solution?
A: Use either the 3/4 value rose or the one from
@Lowlight to do an estimation, practice sound fundamentals so you can see your splash (if conditions allow), and then use the calibrated ruler three inches in front of your face to make a correction. But that doesn't work in all situations because:
- You're at a match where you're not allowed to shoot at the same target twice, and the DoF varies a lot in the stage.
- You're shooting at an animal and aren't suppressed.
- You're shooting at a human who doesn't live by inshallah (or, "I don't need to duck because if it's God's will I get killed, I'll get my 72 virgins and finally get laid") and will therefore hide behind a rock when he hears the first splash.
B: Get a good reading with a Kestrel and enter the relevant data into a ballistic computer. I used to use a ConX/Kestrel setup and now use a TerrapinX/Kestrel setup. In the match I shot Sunday, I had pre-printed labels with the target locations and distances for my arm band. I lazed every target while I was in the hole and wrote the elevation and windage (and corrected distance if I saw a difference from the match book) on the label and dialed those numbers. I was the worst shooter in my squad by a good margin (I really suck at positional shooting), but got the highest score in the squad on the stage that had the worst wind. One of the targets was at a 15-20 degree angle down. The Kestrel/TerrapinX accounted for that, and several of the other shooters were high. So there's that.
C: Combine A&B by using a rose if the wind is close to full value, and use a Kestrel if it's not.
Lastly, a little bit about the "physicist" answers: We don't shoot "perfectly spherical bullets" We shoot G7 bullets. So, even with a perfect wind and DoF vector (meaning both the velocity and direction estimation are perfect), we are still not accounting for the full value wind moving across the length of the bullet and the no-value wind pushing at the tail or the tip of the bullet, which each have different drags. That still doesn't change the solutions above.